Teorema de Pitágoras. Problemas reales

Aprendizaje esperado: Resuelve problemas que implican el uso del teorema de Pitágoras.

Énfasis: Resolver problemas reales que impliquen el uso del teorema de Pitágoras.

¿Qué vamos a aprender?

Resolverás problemas cuadráticos usando la factorización, empleando el método de factor común en problemas geométricos.

Posteriormente, trabajarás con problemas de factorización utilizando el factor común en problemas reales; binomios conjugados (diferencia de cuadrados), dos binomios con un término común y desarrollo del binomio al cuadrado, tanto en problemas geométricos como reales.

Necesitarás tu cuaderno, lápiz, juego de geometría y tu libro de texto.

En caso de que no cuentas con el libro, tienes la opción de consultarlo a través de la página de la Comisión Nacional de Libros de Texto Gratuitos.

Anota las dudas, inquietudes o dificultades que surjan al resolver los planteamientos.

¿Qué hacemos?

El tema de solución de problemas de ecuaciones cuadráticas lo habías abordado en sesiones anteriores, pero por métodos informales y por operaciones inversas. Ahora lo trabajarás con ecuaciones de segundo grado por el método de factorización.

Pero antes de empezar con el tema, lee el siguiente cuento:

Érase una vez, en una escuela secundaria en México, en específico en un salón de tercer grado, grupo…, bueno, algún grupo.

Había un estante en el salón lleno de materiales, hojas, plumones, dados, ligas y tarjetas de diversos tamaños, colores, formas y contenido.

Debido a una pandemia mundial, el salón estaba vacío desde hace medio año y las tarjetas, que eran las más inquietas de los materiales, se empezaron a preguntar: “las vacaciones ya duraron mucho, ¿no creen?, ¿cuándo nos sacarán de este encierro?”, entre otras miles de preguntas, generando cada vez más angustia entre las tarjetas.

Al notar la situación, una de las tarjetas les propuso a las demás hacer diferentes juegos que las mantuvieran ocupadas, entretenidas y se divirtieran todas juntas.

Así que decidieron empezar a jugar reuniéndose en grupos, dependiendo de sus:

1. Colores

2. Tamaños

3. Formas

Pero todos los grupos de tarjetas eran muy diferentes entre sí, ya que los criterios que decidieron las separaban en lugar de integrarlas. Se acomodaban muy rápido y empezaban a aburrirse rápidamente.

Fue entonces que una sabia tarjeta, un poco desgastada, les propuso el reto de formar grupos mixtos dependiendo de su contenido, ya que algunas tenían como contenido monomios, polinomios, expresiones cuadráticas, etc. Ahora se deberían acomodar de acuerdo con los siguientes grupos:

Grupo 1. Factor común

Grupo 2. Diferencia de cuadrados

Grupo 3. Binomios con un factor común

Grupo 4. Trinomio cuadrado

Es decir, dependiendo del contenido de cada tarjeta, se deben acomodar en un grupo por el método de factorización que le corresponde a cada una. Entonces, las tarjetas estuvieron jugando hasta que se terminó la pandemia y las clases se reanudaron.

¿El cuento te recordó algo parecido a la realidad?

Las tarjetas del cuento, en un inicio, se tardaron un poco en ubicar su grupo, ya que no sabían:

• ¿Qué es factorizar?
• ¿Cuáles son los métodos de factorización?
• ¿Qué es un factor común?, entre otras preguntas.

La factorización es el proceso de presentar una expresión matemática o un número en forma de multiplicación. Recuerda que los factores son los elementos de la multiplicación y el resultado se conoce como producto.

La factorización descompone una expresión algebraica en factores para presentarla de una manera más simple.

Se dice que un polinomio tiene factor común cuando existe un factor que se repita en los diferentes términos, es decir, cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.

Lo primero que vas a recordar es la diferencia que existe entre el mínimo común múltiplo (mcm) y el máximo común divisor (MCD).

Primero, los números primos, son aquellos números que sólo se dividen entre sí mismos y la unidad.

Observa el siguiente ejemplo:

Como 2, que es el único primo par, 3, 5, 7, 11, 13, 17, entre otros.

Todo número natural es primo o producto de primos. Por ejemplo, 8, que no es primo, es producto de primos, específicamente, varias veces el número 2; 8 es igual a 2 por 2 por 2. El número 15 es producto de 5 y 3.

El mínimo común múltiplo es representado por sus abreviaturas mcm. El mínimo común múltiplo es el número positivo más pequeño que es múltiplo de dos o más números.

Para calcular el mínimo común múltiplo de dos o más números, comienza por descomponer esos números en números primos.

Observa un ejemplo:

Suponiendo que tienes el siguiente binomio 10”xy” al cuadrado + 25”x” al cubo “y” al cuadrado, y lo que harás será tomar los coeficientes 10 y 25 para saber cuál es su mínimo común múltiplo.

Debes ir obteniendo los números primos de cada coeficiente, primero obtienes la mitad, para el 10 sería 5 y como 25 no tiene, solamente lo bajas; después, verifica si se puede dividir entre 3, pero ni el 5 ni el 25 pueden dividirse entre 3, por lo que sigues con el siguiente número primo, el 5, y verifica si se puede dividir entre 5, para el número 5 sería 1 y para 25 sería 5. Lo último que falta es verificar si se pueden dividir nuevamente entre 5 para que llegues a la mínima expresión, que es 1.

Los factores que obtienes, los multiplicas, es decir, 2 por 5 por 5 y obtienes que el mínimo común múltiplo para los factores 10 y 25 es 50.

Esto quiere decir que, entre los múltiplos de 10 y de los múltiplos de 25, el 50 es el primer número en común.

Por otro lado, el Máximo Común Divisor, que se representa por sus iniciales en mayúsculas MCD, es el mayor número que divide exactamente dos o más números a la vez. Cuando se habla del mayor número, sólo tienes en cuenta los divisores positivos.

También puedes decir que el máximo común divisor de dos números “A” y “B”, es el número mayor que los divide a los dos, tanto al número A como al número B.

Observa un ejemplo:

Toma el mismo binomio 10“xy” al cuadrado + 25“x” al cubo “y” al cuadrado; en este caso, también tomarás los coeficientes 10 y 25, sólo que, en esta ocasión, los utilizarás para saber cuál es su Máximo Común Divisor.

Lo que harás es ir obteniendo los números primos de cada coeficiente: primero buscarás si se pueden dividir entre 2, es decir, si tienen mitad, luego si se pueden dividir entre 3 y luego entre 5, y así sucesivamente. Pero, a diferencia del mínimo común múltiplo, todos los valores deben tener lo mismo para ambos coeficientes. El 10 y el 25 se pueden dividir entre 5, pues 10 es igual a 5 por 2 y 25 es igual a 5 por 5. El 10 puede dividirse entre 2, pero el 25 no.

Para este caso, sólo obtiene un factor, por lo que el Máximo Común Divisor es 5.

Para resolver problemas cuadráticos usando factorización por medio de factor común, utilizarás el Máximo Común divisor (MCD).

Eso, en cuanto a la parte de los coeficientes, pero ¿qué hay de la base o literal?, ¿cómo los factorizas?

Recuerda que cada término algebraico tiene cuatro componentes: el signo, el coeficiente, la base o literal y el exponente.

Observa un ejemplo:

Para 10 “xy” al cuadrado. El signo sería positivo (recuerda que, en este caso, aunque no lo escribas, sabes que es positivo).

El coeficiente es 10. La literal es “xy”. Y el exponente es 2 porque está elevado al cuadrado.

Para descomponer en factores el binomio, se descomponen los factores de manera separada, es decir, hacer la factorización en primos de los coeficientes y, para las literales, lo único que harás será descomponer en factores según lo indique el exponente de cada literal.

Observa el siguiente ejemplo:

Tienes el siguiente binomio: 10“xy” al cuadrado + 25“x” al cubo “y” al cuadrado. Primero trabajarás sobre el primer monomio.

Para el número 10, su factorización en primos es 2 por 5. Continua con los demás elementos del término algebraico: la letra "x" no está siendo multiplicada por nada, y como su exponente es 1, entonces simplemente queda como una "x". Por otro lado, la letra "y" está al cuadrado, entonces la descomponemos como "y" por "y". Recuerda que elevar al cuadrado es lo mismo que multiplicar por sí mismo dos veces esa misma literal.

Ahora haz lo mismo con el siguiente término del binomio.

Para el 25, su factorización en primos es 5 por 5; continuando con las literales tienes "x" al cubo, entonces "x" al cubo es "x" por "x" por "x". Recuerda que el exponente te indica cuántas veces vas a multiplicar por sí misma la base; para la literal "y", está al cuadrado, entonces quedaría "y" por "y".

Es decir, que lo único que estás haciendo es la factorización en primos del número, con la factorización de la base.

Ahora conocerás cómo calcular el máximo común divisor de los monomios. Sólo hay que ver cuáles de estos números y variables están en ambos.

Para los monomios 10“xy” al cuadrado y 25“x” al cubo “y” al cuadrado, tienes que el factor común entre ambos monomios en la parte numérica es el 5, y por la parte literal, el factor común sería solamente una “x”, y para la literal “y” serían 2 las que están en común.

Por lo tanto, el Máximo Común Divisor es la multiplicación de estos factores, o sea que sería 5 por "x" por "y" por "y", lo cual quedaría expresado como 5“xy” al cuadrado.

Y ahora, el binomio 10“xy” al cuadrado + 25“x” al cubo “y” al cuadrado, con el que empezaste.  Ahora que ya conoces su factor común, lo puedes escribir como:

10 “xy” al cuadrado + 25 “x” al cubo “y” al cuadrado = a 5 “xy” al cuadrado por 2 + 5 “x” al cuadrado.

A continuación, te presentaremos algunas situaciones que resolverás para conocer más de este tema. Puedes desarrollar el tema con modelos geométricos, que te permita factorizar por el método del factor común.

Inicia con el planteamiento de los siguientes problemas:

Situación 1:

Dibuja en tu cuaderno la siguiente figura geométrica, la cual es un rectángulo.

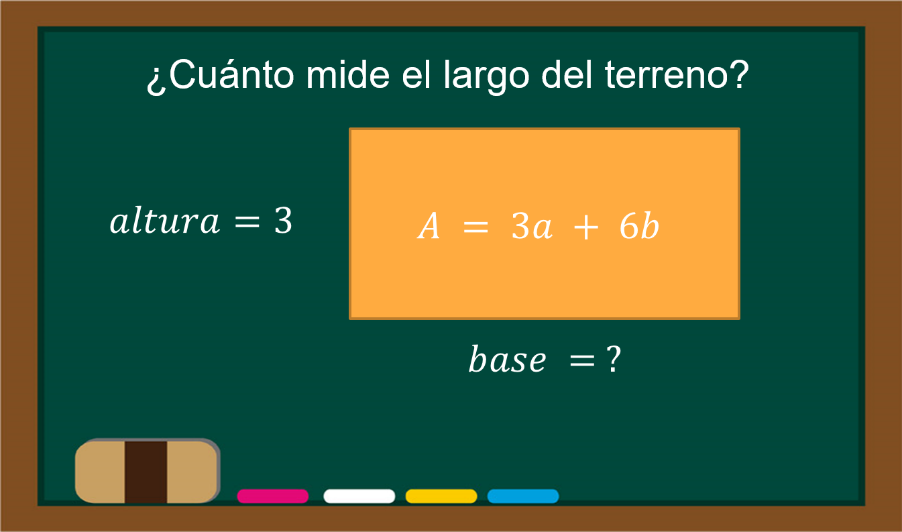
El rectángulo tiene un área de 3a + 6b, si su altura mide 3 unidades, ¿cuánto mide su base?

Expresa en tu cuaderno tu resultado como el producto de factores. ¿Por qué como el producto de dos factores? Porque el área de un rectángulo es base por altura; dos cantidades.

Aplica la factorización por factor común al área de 3a + 6b, si sabes que la altura es de 3 unidades y el área de un rectángulo es base por altura, obtiene que el producto de 3 por a da 3a y 3 por 2b resulta 6b, por lo tanto, 3 es la altura y el factor común y la base del rectángulo es a+2b.

Situación 2:

Jacinta e Isidro son alumnos de la Telesecundaria Hermenegildo Galeana, en Teacalco, estado de Guerrero. Están construyendo un modelo geométrico para mostrárselo a su maestra, el cual es un modelo rectangular; este modelo se debe dividir de tal forma que se utilice la totalidad del área. Una de las condiciones es que se respeten los siguientes modelos para la construcción:

El primer modelo A es un cuadrado de lado “x”, el modelo B, un rectángulo de base “y” y altura “x”.  Te solicitan que se cubra el modelo geométrico con las siguientes características:

Dos cuadrados tipo A, 6 rectángulos tipo B y, que indiques: ¿cuánto mide la altura y la base del rectángulo? ¿Qué arreglo le propones a la constructora?

Inicia con el arreglo de los modelos geométricos. ¿Cómo los acomodarías? Recuerda: son 2 modelos tipo A y 6 modelos tipo B.

Todos en línea. Su altura mide “x”, la base mide 2x + 6y, con un área de 2“x” al cuadrado + 6xy.

Con esa área, puedes proponer otro arreglo. ¿Podrías plantear de qué otra manera Jacinta e Isidro hicieron el arreglo?

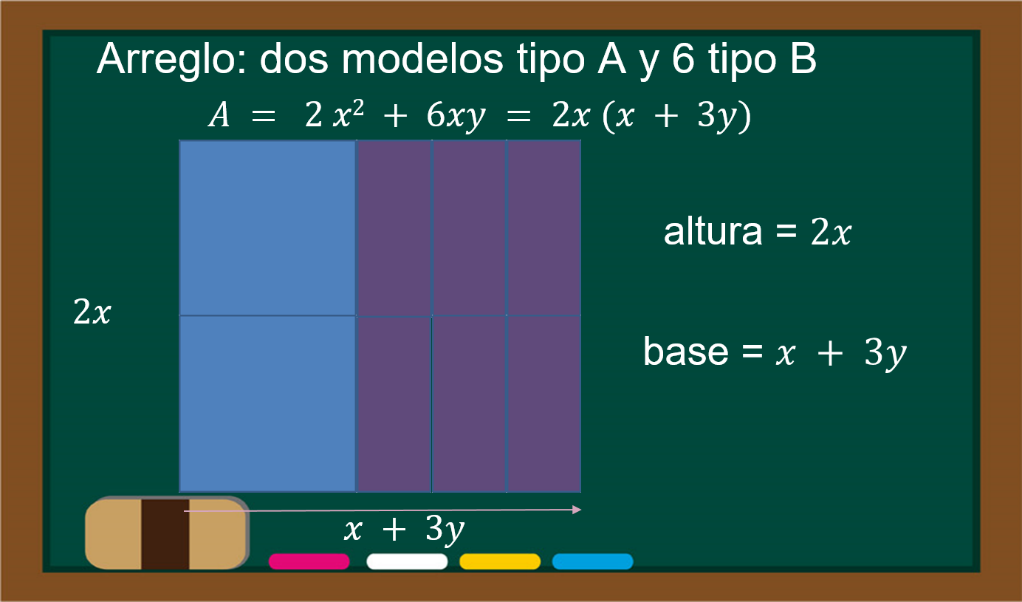
Ellos plantearon: si el área es de 2“x” al cuadrado + 6xy, se aplica la factorización por factor común de la expresión y se obtiene que, de los números 2 y 6, su máximo común divisor es 2; de las literales x al cuadrado y “xy” es “x”, por lo tanto, la altura mide 2x y la base mide los términos necesarios para completar el área, que son x + 3y.

Jacinta e Isidro, con este modelo geométrico, siguen manteniendo las mismas condiciones, respetando los modelos de un inicio, el del tipo A y B.

La expresión del área del rectángulo, si la observas con atención, se trata de una ecuación de segundo grado de la forma “ax” al cuadrado + bx, que se resolvió por el método de factorización por factor común.

Observa otro arreglo diferente:

Jacinta e Isidro ahora solicitan un arreglo de 8 modelos del tipo A y 12 modelos del tipo B. Partiendo del conocimiento del área del arreglo solicitado, tienes 8 del tipo A, son 8x2 más 12 de tipo B, sería 12xy, es decir, A = 8“x” al cuadrado + 12xy.

Con un área de 8“x” al cuadrado +12xy, aplicando la factorización por factor común, primero calcula el MCD de los números 8 y 12, que es 4, de las literales “x” al cuadrado y “xy” su factor común es x. Por lo tanto, al juntar ambos, es 4x, el cual se debe multiplicar por (2x + 3y) para completar el área total.

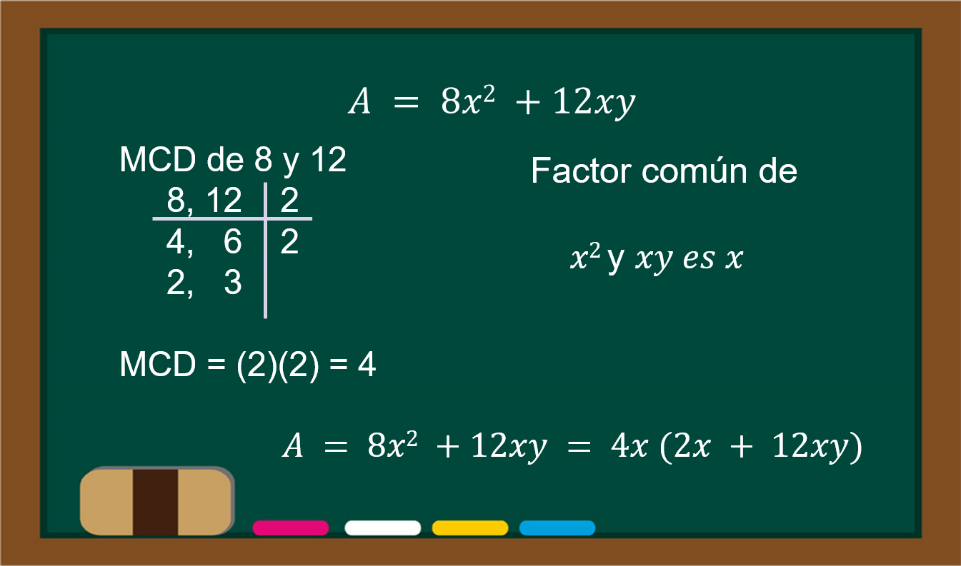
Recuerda que para calcular el MCD, también se puede obtener por el producto de los factores primos de 8 y 12 y multiplicar los que tienes en común, que son 2 y 2. Si observas, es 4 y, de las literales, se considera la de menor exponente y que se encuentre en ambos términos, la cual es “x”. Por lo anterior, obtienes que el factor común es 4x, que al multiplicarse por 2x + 3y, da por resultado el área del rectángulo.

Observa un último arreglo geométrico que hicieron Jacinta e Isidro, en donde solicitan el valor de la altura y la base.

Observa bien el siguiente inciso.

El arreglo que proponen es:

a) 20“x” al cuadrado + 18x, si calculas el MCD de (20, 18), es 2, y de la parte literal tienes a “x” como factor común. Por lo tanto, obtienes 2x (10x + 9). Recuerda, los coeficientes que se escriben entre paréntesis son los que sobran del cálculo del MCD. Del rectángulo, tienes que la altura es de 2x y la base 10x + 9.

Ahora factoriza las siguientes expresiones algebraicas:

a) 5“x” al cuadrado -15x

Resuelve esta ecuación por medio de los factores primos de los números; de 5 es 5 y de 15 es 3 por 5, el MCD de ambos es 5 y, de la parte literal, es “x”, por lo tanto, los factores son 5x por x -3.

Observa la siguiente ecuación:

b) 12“x” al cuadrado - 4x

Calculando el MCD por el producto de factores primos, tienes que de 12 es 2 por 2 por 3 y de 4 es 2 por 2, de los que tienen en común son 2 por 2 = 4 y de la parte literal, es x, obtienes 4x (3x - 1).

c) 18“x” al cuadrado - 24x

Realiza el cálculo del MCD por la descomposición de factores; tienes que el MCD de (18, 24) es 2 por 3 = 6 y, de las literales, es “x”, por lo tanto, resulta 6x (3x - 4).

Jacinta e Isidro propusieron cuatro ecuaciones de segundo grado, con las que podría quedar más clara la factorización por factor común.

Retomando el procedimiento, tienes que: Primero, la expresión se debe encontrar igualada a cero. Después se calcula el MCD de los coeficientes de la expresión y de las literales se considera la de menor exponente. Posteriormente, se expresa como producto el factor común y el binomio que completa la expresión.

Para resolver la ecuación de segundo grado del tipo a“x” al cuadrado + bx, después de la factorización, sólo debes igualar a cero cada uno de los factores y despejar las ecuaciones resultantes, obteniendo así las dos soluciones que corresponden a una ecuación de este tipo. Para que quede más claro este procedimiento, considera el último arreglo que propusieron Jacinta e Isidro. Observa:

Recuerda que el arreglo propuesto es: 18“x” al cuadrado - 24x; al factorizar obtienes 6x (3x - 4). Ahora separa los factores y los igualas con cero, obteniendo dos ecuaciones lineales, las cuales, al despejarlas, tienes que en 6x = 0, se divide entre 6 ambos miembros, eliminando los 6 en el primer miembro al ser operaciones inversas y, en el segundo miembro, al realizar la operación, obtienes 0, por lo que equis uno es igual a cero y en la ecuación 3x - 4 = 0.

Para resolverla, agrega la operación inversa en ambos miembros, es decir, suma 4; en el primer miembro se anulan los 4 y en el segundo miembro se suma 0 + 4, posteriormente, divide entre 3 ambos miembros, anulando los 3 en el primer miembro, por ser operaciones inversas, teniendo como resultado que equis dos = 4/3.

Para el arreglo propuesto, es: 12“x” al cuadrado - 4x; al factorizar, obtienes 4x (3x - 1). Ahora separa los factores y los igualas con cero, obteniendo dos ecuaciones lineales, las cuales, al despejarlas, tienes en 4x = 0; se dividen entre 4 ambos miembros, eliminándose los 4 en el primer miembro al ser operaciones inversas y, en el segundo miembro, al realizar la operación, obtienes 0, por lo que, a x1 = 0 y en la ecuación 3x - 1 = 0; para resolverla, agregas la operación inversa en ambos miembros, es decir, sumas 1; en el primer miembro se anulan los 1, y en el segundo miembro se suma 0 + 1, posteriormente divides entre 3 ambos miembros, anulando los 3 en el primer miembro, por ser operaciones inversas, teniendo como resultado que x2 = 1/3.

Ya resolviste una ecuación de segundo grado del tipo a“x” al cuadrado + bx por factorización por factor común con sus dos soluciones.

El Reto de Hoy:

Plantea y resuelve los siguientes problemas utilizando lo que acabas de aprender.

1. El área de un cuadrado es igual a 8 veces la medida de su lado, ¿cuánto mide por lado el cuadrado?

2. El triple del área de un cuadrado menos seis veces la medida de su lado es igual a cero. ¿Cuánto mide por lado el cuadrado?

Debes tener en cuenta lo que has aprendido durante las siguientes sesiones; todo esto te servirá para entender mejor. Así que revisa lo aprendido para seguir avanzando.

Recuerda que estudiaste problemas cuadráticos usando la factorización, empleando la técnica de factor común en problemas geométricos.

Conociste cuál es el significado de la factorización, el cual es el proceso de presentar una expresión matemática o un número en forma de multiplicación. También recordaste que los factores son los elementos de la multiplicación y el resultado se conoce como producto.

Es importante que recuerdes que el objetivo de la factorización es descomponer una expresión algebraica en factores para presentarla de una manera más simple.

Busca en tu libro de texto de Matemáticas de tercer grado problemas y ejercicios similares a los que estudiaste, para que los resuelvas y practiques lo que aprendiste.

Descarga tu clase dando clic

¡Buen trabajo!

Gracias por tu esfuerzo.