Encontrando ecuaciones cuadráticas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22Aprendizaje esperado: l ee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: analizar las diferentes representaciones de una relación cuadrática. Partir del registro tabular .
¿Qué vamos a aprender?
Es importante que, conforme se vayan presentando las distintas actividades, vayas realizándolas, así como tomar notas en tu cuaderno de lo que aprendes, además de tus dudas en torno a esta sesión.
Irás paso a paso, identificando y reflexionando sobre las diferentes representaciones de una relación de variación cuadrática, a partir de su expresión algebraica .
Ten a la mano tu cuaderno, regla, lápiz o bolígrafo y lápices de colores.
¿Qué hacemos?
Inicia respondiendo las siguientes preguntas.
¿Dónde se ubica el punto A

Donde está el punto negro , y lo escribes como A.
Ya que, primero, avanzas 2 lugares a la derecha del origen y luego, avanzas 3 lugares hacia arriba, y encuentras la ubicación del punto A.
¿Dónde se ubica el punto B (-2, 3)?
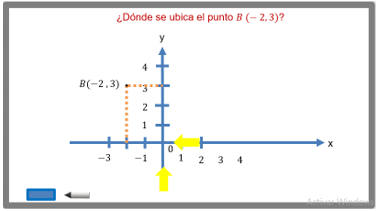
Donde está el punto negro , y lo escribes como B.
Ya que primero avanzas 2 lugares a la izquierda del origen y, luego, avanzas 3 lugares hacia arriba,
¿Dónde se ubica el punto C (- 2, - 3)?
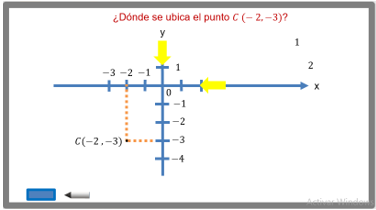
Donde está el punto negro , y lo escribes como C.
Avanzas 2 lugares a la izquierda del origen, luego avanzas 3 lugares hacia abajo, y encuentras la ubicación del punto C.
¿Dónde se ubica el punto D (2, - 3)?
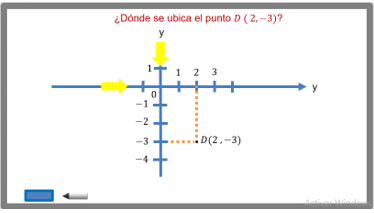
Donde está el punto negro , y lo escribes como D.
Avanzas 2 lugares a la derecha del origen, luego avanzas 3 lugares hacia abajo y encuentras la ubicación del punto D.
Ésa fue la primera parte, continúa con la segunda.
Observa las siguientes ecuaciones:

¿Cómo puedes hacer para encontrar el valor de a, b y c?
Observa ¿Puedes resolver a+b+c=40?
No puedes resolver la ecuación a + b + c = 40, ya que, no conoces el valor de a, de b, o de c.
Tampoco puedes resolver la ecuación 3 a + b = 37, ya que no conoces el valor de a o de b.
Sin embargo, sí puedes resolver la ecuación
2a = 18
¿Cómo lo haces?
¿Cómo se resuelve 2a=18?
Divide entre 2 ambos miembros de la igualdad: 2a/2 = 18/2
2 entre 2 es uno y, uno a no se escribe, sólo se escribe a. Por lo que queda: a = 18/2
¿Cuánto vale a?
18 entre dos es nueve. Entonces , a = 9
Ahora conoces el valor de a. a = 9.
¿qué puedes hacer ahora que conoces el valor de a?
Con el valor de a puedes conocer el valor de b en la ecuación 3a + b = 37.
¿Cuánto vale b?
Al sustituir a por 9, tienes:

3 (9) + b = 37
Como 3 x 9 = 27 obtendrás:
27 + b = 37
Restas 27 en ambos miembros de la igualdad
27 + b – 27 = 37 – 27
b = 10
Ya conoces el valor de b.
Ahora sabes que a = 9 , y b = 10 .
¿Con estos valores, puedes conocer el valor de c en la ecuación:
a + b + c = 40?
¿Cuánto vale c?
Observa, al sustituir a = 9 y b = 10 en la ecuación , tienes:

9 + 10 + c = 40
Luego, como 9 + 10 es 19 tienes:
19 + c = 40
Restas 19 en ambos miembros de la igualdad :
19 + c – 19 = 40 – 19
c = 21
Por fin, logras conocer el valor de a, b y c, y resolver las tres ecuaciones.
Ahora, continúa con la tercera parte .
Considera la siguiente expresión algebraica de segundo grado:
ax^2 + bx + c
Si a = 9, b = 10 y c = 21, al sustituir los valores de a, b y c encontrados en la pregunta anterior, ¿cuál es la expresión algebraica que se obtiene?
Debes sustituir los valores encontrados anteriormente en la expresión algebraica.
Al sustituir los valores, ¿cómo queda e sta expresión algebraica de segundo grado?

Queda:
9x^2 + 10x + 21
Pasa a la última pregunta:
¿Cuál es el valor numérico de la expresión 9x^2 + 10x + 21, cuando x = 5?
Observa, hay que sustituir valores :

9(5)
Ya sabes qué; 5
9(25) + 50 + 21 =
Luego: 9(25) = 225
225 + 50 +21 =
Al final sumas y tienes: 296 .
Es decir, para x = 5 : 9x^2 + 10x + 21= 296
Aprende cómo graficar una expresión cuadrática , si conoces la tabla de valores.
Tienes la siguiente tabla:
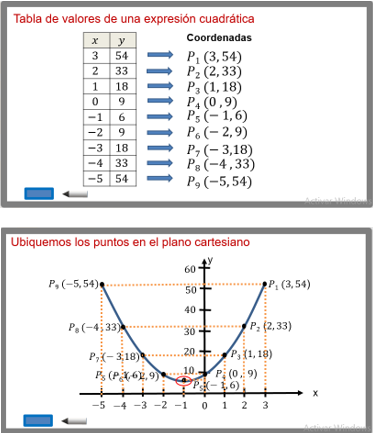
P1 (3, 54), avanz
as
3 lugares a la derecha del origen
,
y 54 lugares
P2 (2, 33), avanzas 2 lugares a la derecha del origen , y 33 lugares arriba.
P3 (1, 18), avanzas 1 lugar a la derecha del origen , y 18 lugares arriba.
P4 (0, 9), como la primera coordenada es cero, no se moverá a la derecha ni a la izquierda, permanecerá en el origen, pero avanzamos 9 lugares arriba , conforme a la segunda coordenada.
P5 (- 1, 6), avanzas 1 lugar a la izquierda del origen , y 6 lugares arriba.
P6 (- 2, 9), avanzas 2 lugares a la izquierda del origen , y 9 lugares arriba.
P7 (- 3,18), avanzas 3 lugares a la izquierda del origen , y 18 lugares arriba.
P8 (-4, 33), avanzas 4 lugares a la izquierda del origen , y 33 lugares arriba.
P9 (-5, 54), avanzas 5 lugares a la izquierda del origen , y 33 lugares arriba.
La figura es una curva que se denomina parábola.
¿Cuál es el vértice?
El vértice es el punto de inflexión o de cambio de la curva. En este caso , es el punto P5 (- 1, 6).
Al graficar los puntos , sabes que es una ecuación cuadrática.
Con los datos de la tabla , encuentra la ecuación que corresponde a la tabla de valores.
Una ecuación cuadrática es de la forma:
y = ax^2 + bx + c
Entonces , hay que encontrar los valores de a, b y c.
Analiza los valores de la siguiente tabla:

Cuando x = 0, ¿cuánto vale “y”?
“y” es igual a 9.
Sustituye esos valores en la ecuación.
Entonces y = ax^2+bx+c, queda como
9 = a(0)^2 + b(0) + c
9=0 +0 +c
9 = c; y así c = 9.
Ya tienes el valor del término independiente, c = 9.
Pero, ¿qué haces con este valor?
Sustituyes el valor de c para encontrar otras expresiones algebraicas.
Y es lo que harás con c.
Sustituye el valor de c , y utiliza los valores de “x” y “y” con otras coordenadas.
Ocupa primero la coordenada (1,18).
¿Qué significa esto?
Que cuando x = 1, y= 18.
Correcto. Sustituye los valores y , ¿Qué resulta de ello?
En la ecuación de la forma y=ax^2+bx+c, al sustituir los valores “x” igual a 1 , y “y” igual a 18, tienes que :
18 = a(1)^2 + b(1) + 9
Entonces, 18 = a+b+9.
Pasa a un miembro los términos constantes y
A esta expresión la llamarás " Ecuación 1 ".

Ahora ocupa otra coordenada, que se
En la ecuación de la forma y=ax^2+bx+c, al sustituir los valores “x” igual a -1 , y “y” igual a 6, tienes que :
6=a(-1)^2 + b(-1) + 9
Entonces, 6 = a-b+9.
Pasas a un miembro los términos constantes y
A esta expresión la llamarás " Ecuación 2 ".
Tienes estas dos ecuaciones:

9=a+b y -3=a-b.
Despejas “a”
En la Ecuación 1 :
9 = a+b
Restas b en ambos miembros de la ecuación, y queda :
9-b=a+b-b, queda 9-b=a, por lo tanto, a = 9-b .
Despeja a de la Ecuación 2,
En la Ecuación 2 :
-3 = a-b
Sumas b en ambos miembros de la ecuación, y queda :
-3+b=a-b+b, queda -3+b=a, por lo tanto, a = -3+b
Ahora , iguala “a” de ambas ecuaciones , y queda :
9-b=-3+b
Observa que ahora sólo tienes una incógnita.
¿Qué haces ahora?

Encontrar el valor de b,
Tienes dos expresiones que puedes igualar entre sí, ya que “a” esta despejada en ambas expresiones:
9 – b = -3 + b ; sumas en ambos miembros de la ecuación “b”, y queda:
9 – b + b = -3 + b
Esto queda como 9=-3+2b .
S umas a ambos miembros de la ecuación “3”, y queda :
9+3=-3+2b+3,
Haces las operaciones, y queda
12=2b
Divide entre dos a ambos miembros de la ecuación :
12/2=2b/2, y queda al final que b = 6.
Ya tienes que “b” es igual a 6.
Sólo queda encontrar el valor de “a”.
Pero ya tienes dos ecuaciones que definen a “a”. Selecciona una de ellas.
Ocupa la Ecuación 1, cuando a = 9-b.
Sustituye el valor de b = 6, y a = 9 – 6. Por lo tanto, a = 3.

Sustituye los valores de “a”, “b” y “c” en la forma y=ax^2+bx+c .

Al sustituir; a = 3, b = 6 y c = 9 en la ecuación , obtienes:
y = ax^2 + bx + c
y = 3x^2 + 6x + 9
Para despejar algunas dudas, realiza otro ejercicio.
En el siguiente ejercicio obtendrás una ecuación cuadrática, si conoces la tabla de valores.
Con la siguiente información, encuentra la expresión algebraica que la contenga.
Primero, traza la gráfica.
Las coordenadas de los puntos quedan así:
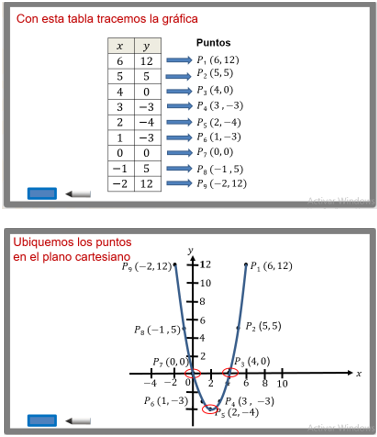
Observa que la parábola corta al eje de las “xs” en los puntos:
P3 (4, 0) y P7 (0, 0).
Observa que el vértice de la parábola es el punto P5 (2, - 4).
¿Cómo encontrarás la ecuación que contenga los puntos de esta gráfica?
Observa que es la gráfica de una ecuación cuadrática.
Lo sabes, porque es una parábola y las parábolas se pueden representar con una ecuación cuadrática.
L que haces es sustituir los valores de “x” y “y” de algunas coordenadas, en la ecuación y=ax^2 + bx+c.

Cuando x= 0, ¿cuánto vale “y”?
“y” es igual a 0.
Sustituye esos valores en la ecuación.
Entonces y = ax^2+bx+c, queda como :
0 = a(0)^2 + b(0) + c
0=0 +0 +c
0 = c; y así c =0.
Ya tienes el valor del término independiente, c = 0 .
Sustituyes el valor de c para encontrar otras expresiones algebraicas.
S ustituye el valor de c y utiliza los valores de “x” y “y” con otras coordenadas.
Ocupa primero la coordenada (1, -3).
Significa que cuando x = 1, y= -3.
Sustituye los valores y ¿Qué resulta de ello?
En la ecuación de la forma y=ax^2+bx+c, al sustituir los valores “x” igual a 1 , y “y” igual a -3, tienes que :
-3=a(1)^2 + b(1) + 0
Entonces, -3 = a+b.
Queda, a+b=-3
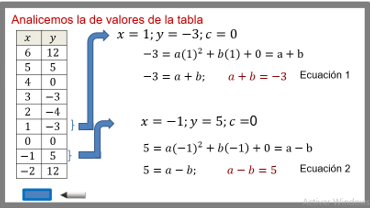
A esta expresión la llamarás Ecuación 1.
Ocupa otra coordenada,
En la ecuación de la forma y=ax^2+bx+c, al sustituir los valores “x” igual a -1 , y “y” igual a 5, tienes que :
5=a(-1)^2 + b(-1) + 0
Entonces, 5 =
Queda, a-b=5.
A esta expresión la llamarás " Ecuación 2 ".
Tienes estas dos ecuaciones:
a+b=-3 y a-b=5.
Despeja “a” en ambas ecuaciones :
Resta b en ambos miembros de la ecuación, y queda :
a+b-b=-3-b, por lo tanto, a=-3-b.

Despeja a de la Ecuación 2 . a-b= 5
Suma b en ambos miembros de la ecuación, y queda : a-b+b=5+b, por lo tanto, a = 5+b .
Ahora

Entonces, -3-b=5+b
Sumas
Esto queda como -3=5+2b
Restas “5” en
ambos miembros de la ecuación y queda
:
-3-5=
Haces las operaciones y queda : -8=2b
Divides entre dos a ambos miembros de la ecuación
Ya tienes a “b” , y es igual a -4.
Sólo queda encontrar el valor de “a”.
Ocupa una de las dos ecuaciones que definen a “a” . Selecciona una de ellas
Ocupa la Ecuación 1, cuando a =-3-b .
Sustituye el valor de b=-4, y a=-3- (-4). Por lo tanto, a = -3+4 , = 1.

“a” es igual a 1.
Sólo hace falta s ustituir los valores de “a”, “b” y “c” en la forma y=ax^2+bx+c .
Al sustituir a = 1, b = -4 y c = 0 en la ecuación , obtienes:
y = ax
y = x

Debes sentirte más seguro para graficar y obtener una ecuación cuadrática a partir de un registro tabular.
Recapitula: una relación cuadrática puede representarse por medio de una tabla, una gráfica o una expresión algebraica de segundo grado.
Dada una tabla de valores e identificando por su gráfica que es una relación cuadrática, puedes encontrar la ecuación que contenga dichos puntos.
Y que las gráficas que estudias se llaman parábolas.
El reto de hoy:
Resuelve algunos problemas que están en tu libro de texto. También te sugerimos pensar en que otras áreas del conocimiento se pueden emplear estas relaciones cuadráticas .
Cada vez que resuelves problemas de matemáticas, tus conocimientos se hacen más útiles y duraderos.
¡Buen trabajo!
Gracias por tu esfuerzo .
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/secundaria.html


Login to join the discussion