Recordando el virreinato de la Nueva España I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:17
Recordando el virreinato de la Nueva España I
Aprendizaje esperado: reconoce el proceso de conquista y colonización del México antiguo y la conformación de la Nueva España.
Énfasis: reconocer el proceso de conquista y colonización del México antiguo y el periodo fundacional de la Nueva España.
¿Qué vamos aprender?
El día de hoy iniciarás una serie de tres programas recordando lo aprendido del periodo virreinal. En esta primera sesión abordarás específicamente los acontecimientos acaecidos en la conquista de Tenochtitlan hasta el final siglo XVI.
Debes recordar que el periodo virreinal inició con la conquista de Tenochtitlan el 13 de agosto de 1521, y que los primeros años de dominio español fueron vertiginosos, ya que ocurrieron diversos acontecimientos en la naciente sociedad novohispana.
Para alcanzar el propósito de la sesión, se dividirá en cuatro ámbitos de estudio: político, económico, social y cultural.
Te recomendamos que tengas a la mano una libreta y un bolígrafo para que hagas tus anotaciones, también puedes utilizar tu libro de texto para que consultes imágenes o el tema en particular.
¿Qué hacemos?
Iniciarás la sesión indicando dos conceptos importantes del periodo virreinal: CONQUISTA y COLONIZACIÓN.

https://www.noticonquista.unam.mx/index.php/amoxtli/2380/2372
Conquista se refiere al efecto de controlar, mediante la fuerza armada o militar, un territorio o posesión. Puedes apreciar en la imagen un detalle del Códice Florentino, donde se observa cómo los españoles y sus aliados rompen el cerco mexica en el lago de Texcoco.
En la siguiente imagen la invasión y la conquista se basaron en la violencia, el terror y la crueldad. Se aprecia el códice llamado “Manuscrito del Aperreamiento”, en él observas cómo se utilizaban los perros en la Conquista.

https://www.dimensionantropologica.inah.gob.mx/?p=13100
En esta imagen se define el concepto colonización, que “supone el establecimiento de una colonia o grupo de personas por parte de un país en un territorio no propio, ajeno, lejos de sus fronteras”.

https://www.noticonquista.unam.mx/portada/semanal/1368
En la imagen del Códice Florentino se observa cómo un grupo de españoles, ya establecidos en la Ciudad de México, reciben a un grupo de indígenas.
En la siguiente imagen aprecias el desembarco de algunos colonizadores españoles en el puerto de Veracruz y traen consigo productos y animales nunca antes vistos en Mesoamérica. La introducción de estos productos y animales son considerados también parte de la colonización.

https://www.noticonquista.unam.mx/index.php/imagen-popup/377
Ahora que tenemos más claros los conceptos de conquista y colonización, puedes continuar con el primer ámbito de estudio del periodo virreinal:
ÁMBITO POLÍTICO
Seguramente recuerdan que el ámbito político se refiere a las formas de gobierno y a la organización de las instituciones públicas.
El periodo virreinal inicia con la conquista de México-Tenochtitlan, y un antecedente importante a este hecho son los viajes de exploración.
En 1517 zarpó de Cuba don Francisco Hernández de Córdoba.
En 1518, de la misma isla incursionó Juan de Grijalva.
Y en 1519 Hernán Cortés se dirigió a explorar más allá de Cuba.
Estas tres exploraciones fueron patrocinadas y organizadas por Diego Velázquez, gobernador de Cuba, con quien Hernán Cortés tendría conflictos.
En mayo de 1519 Hernán Cortes se posesionó y fundó el Ayuntamiento de la Villa Rica de la Vera Cruz, con este hecho jurídicamente se independizó de Diego Velázquez.
Por otra parte, desde este lugar Cortés inició formalmente su campaña militar para la invasión y conquista de Tenochtitlan.
En este mapa se traza la ruta que siguió Hernán Cortés para llegar a Tenochtitlan. Con algunos pueblos pudo hacer alianzas para enfrentar a los mexicas.
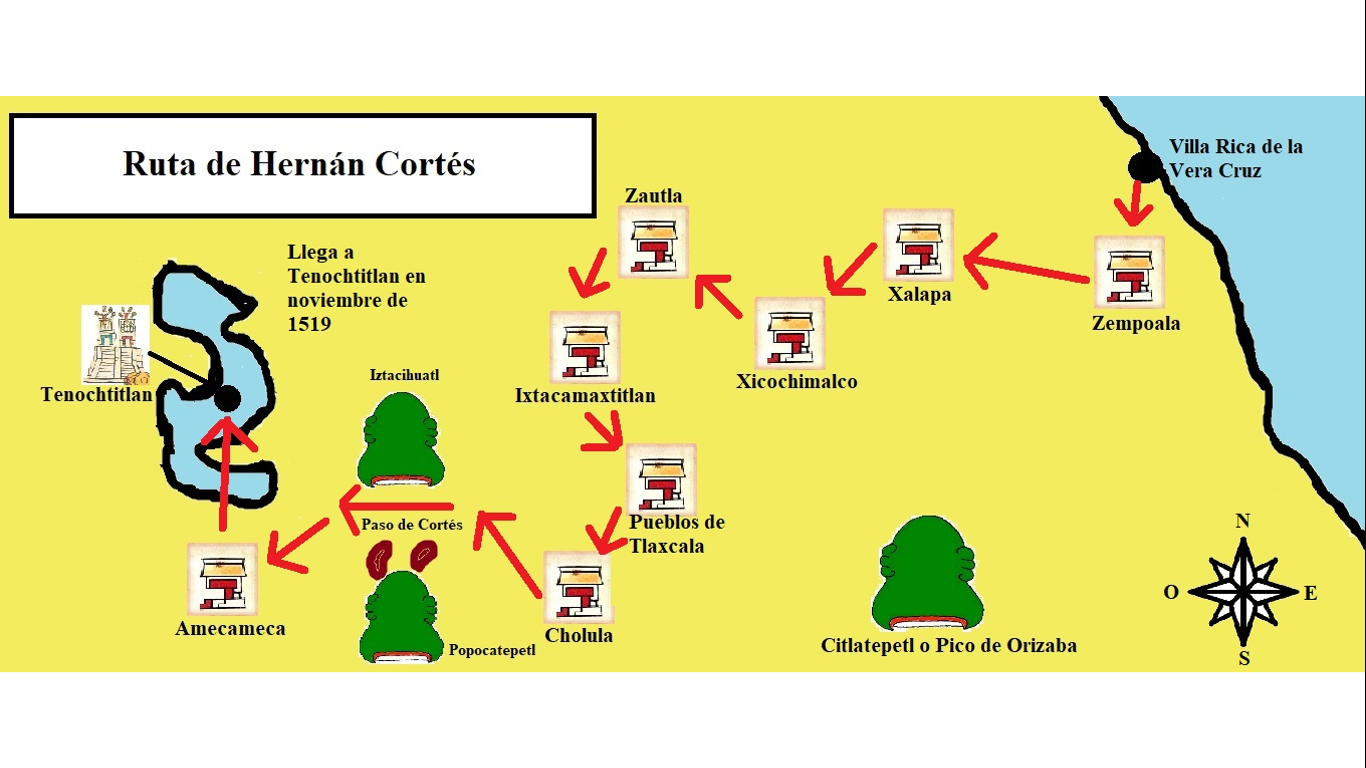
Sin embargo, en Cholula, un pueblo leal y aliado a Tenochtitlan, encontró resistencia, se enfrentaron y el resultado fue una gran matanza de indígenas.
En noviembre de 1519, Cortés, sus soldados y sus aliados llegaron por primera vez a Tenochtitlan y se entrevistaron con Moctezuma, el huey tlatoani de aquella gran ciudad.
Después de la intromisión y llegada de los españoles a la ciudad mexica, Moctezuma les ofreció alojamiento en el palacio de Axayacatl. Pocos días después los españoles lo traicionaron y apresaron para obligar al pueblo mexica a su rendición.
Hernán Cortés viajó de manera imprevista, en 1520, a Veracruz, ya que Diego Velázquez había enviado a Pánfilo de Narváez para apresarlo, pero no lo logró.
Mientras tanto, en Tenochtitlan, Pedro de Alvarado planeó a traición una matanza en el Templo Mayor, como se representa con estas imágenes que pertenecen al Códice Florentino.
Cabe precisar que los mexicas lograron expulsar a los conquistadores de su ciudad.
Después de que Tenochtitlan fue sitiada por los españoles durante varios meses, padeciendo de escasez de alimentos y sin agua potable, los mexicas finalmente cayeron a manos de los conquistadores el 13 de agosto de 1521. Esta fecha es considerada el inicio del periodo virreinal.
No pasó mucho tiempo para que los españoles diseñaran una nueva ciudad, y para 1522 Hernán Cortés recibió de la Corona española el nombramiento como capitán general y gobernador de la Nueva España.
En ese mismo año traslada el Ayuntamiento de la Villa Rica de la Vera Cruz a Coyoacán en donde Cortés establece la sede de su gobierno; con ello sienta las bases de la organización política y administrativa de Nueva España.
De 1522 a 1526 los españoles continuaron el proceso de Conquista: Cortés organizó nuevas expediciones y encargó al capitán Alonso de Ávalos la conquista del territorio de Colima. A Pedro de Alvarado lo comisionó para que explorara y conquistara la región mixteca-zapoteca; su misión se extendería a Chiapas y Guatemala. A Cristóbal de Olid, otro de sus capitanes, le encargó la expedición marítima a Las Hibueras (actual Honduras), mientras que Hernán Cortés partió hacia el sur de Mesoamérica el 12 de octubre de 1524. Por otro lado, Francisco de Montejo logró conquistar el actual Yucatán en 1546.
La organización política de la Nueva España tomó elementos de la estructura de los pueblos mesoamericanos, como los señoríos, así como de la organización política de la metrópoli que ya habían impuesto en otros territorios colonizados, como La Española y Cuba.
Por órdenes reales, en 1527 se crea la Primer Real Audiencia, y en 1532, la Segunda Real Audiencia, con el fin de organizar políticamente los nuevos territorios, pero es en 1535 cuando se funda formalmente el virreinato con el primer virrey Antonio de Mendoza; esta institución política desaparecería en 1821 con la independencia de México.
Ahora inicia el segundo ámbito de estudio:
EL ÁMBITO ECONÓMICO
Recuerda que este ámbito se refiere a la forma en que se produce la riqueza, se comercializa y se distribuye. La primera forma de trabajo impuesta por los conquistadores fue la encomienda, y ésta consistió en repartir señoríos a los conquistadores, a quienes se les denominaba encomenderos.
Los encomenderos recibían del señorío una renta o tributo, que podía cubrirse con metales preciosos, leña, telas, productos agrícolas o mano de obra.
Los encomenderos conservaban gran parte del tributo para sí, y una porción era para la Corona.
El compromiso que los encomenderos tenían era proteger al señorío y evangelizar a sus habitantes. Los encargados de recopilar y entregar el tributo a los conquistadores eran los gobernantes de los pueblos, llamados caciques.
En las siguientes imágenes puedes observar cómo el encomendero recibía el tributo, una parte era para él y otra para la Corona.

En la siguiente imagen se aprecia que, si el tributo era poco o los indígenas no entregaban lo correcto, los españoles los sometían incluso hasta la muerte. Estas imágenes son tomadas del Códice Tepetlaoxtoc.

https://www.noticonquista.unam.mx/imagen-popup/1406
Como puedes apreciar, la primera organización económica tomó como base la organización política del señorío e incluso el cobro de tributos.
Hay que recordar que la principal actividad económica de Mesoamérica fue la agricultura y su principal alimento era el maíz. Con la llegada de los españoles esto cambió, ya que introdujeron nuevos alimentos vegetales y animales de corral.
El cerdo, que fue un animal muy importante porque con su crianza dio inicio a la ganadería menor en Nueva España. Su producción pronto fue tan numerosa que estuvo al alcance de cualquiera. Por su parte, las vacas, cabras y ovejas se introdujeron a Nueva España un poco después, pero hacia 1523 ya se registra su existencia, aunque la cría del ganado mayor se reservó para los españoles.
Respecto a los cultivos, los españoles introdujeron el trigo para elaborar el pan; la caña para la extracción del azúcar y aguardiente; el nogal y el olivo.
Entre las verduras que introdujeron los españoles a México fueron los rábanos, zanahorias, nabos, el ajo, espinaca y cilantro. Entre las frutas se encuentran naranja, durazno, manzana, pera, mandarina, limón, higo y uvas. Para el transporte de estos productos se dejaron de lado a los cargadores o tamemes y se empezaron a utilizar las carretas.
La Conquista y expansión colonial no sólo significó el sometimiento de los indígenas, también implicó el intercambio de plantas y animales, creación de nuevas actividades productivas, el empleo de otras técnicas y herramientas.
Pero la actividad productiva que quizá tuvo mayor impacto en el desarrollo económico y en la transformación del paisaje en la Colonia fue la minería, específicamente, la extracción de la plata.
En 1530 se descubrieron las primeras minas de plata de Nueva España, específicamente, en Taxco, actual territorio del estado de Guerrero. Esto animó a los españoles a explorar otras minas al norte del país. En Zacatecas se encontraron grandes minas de plata y las ciudades de esa región crecieron.
Se puede sintetizar que la minería fue esencial para el crecimiento de las ciudades, la diversificación de actividades y la construcción de templos y caminos, y esto transformó radicalmente el paisaje de Nueva España.
Por otro lado, las rutas comerciales de Nueva España durante el siglo XVI con Europa y Asia fueron dos: la de Veracruz-Sevilla en el océano Atlántico y la de Acapulco-Manila en el océano Pacífico. Nueva España encontró en su metrópoli, España, un freno para desarrollarse comercialmente, con la imposición de reglas duras para no comerciar directamente con naciones europeas e incluso con otras colonias.
El traslado de las mercancías de un continente a otro fue aprovechado por los piratas, quienes robaban los barcos españoles y las riquezas eran trasladadas al país que financiaba la piratería: Inglaterra, Francia u Holanda.
Toda esta efervescencia económica hizo que surgiera en la Ciudad de México un Consulado de Comerciantes, quienes deliberaban asuntos comerciales internos y externos a la Colonia, y su influencia llegó a Sevilla y a Manila.
Hasta aquí el ámbito económico. Ahora revisa: EL ÁMBITO CULTURAL
El ámbito cultural se refiere a las costumbres, las creencias, ideas y formas de entender la vida que hacen al mundo diverso. En el caso de Nueva España, los españoles buscaron eliminar por completo las ideas religiosas de los pueblos mesoamericanos. Prohibieron diferentes rituales como el sacrificio humano; sin embargo, toleraron otras prácticas que se fusionaron con la adoración de los santos católicos.
Después de que los españoles invadieron y conquistaron México-Tenochtitlan, Cortés solicitó al rey que enviara frailes para imponer la enseñanza del cristianismo a los indígenas.
Los frailes tendrían la misión de evangelizar y erradicar las prácticas religiosas prehispánicas: franciscanos, dominicos, agustinos y más tarde los jesuitas, fueron los religiosos que se dieron cita en la colonia.
En 1523 llegaron a la Nueva España los primeros tres frailes franciscanos. Un año más tarde, en 1524, arribaron doce más de esta misma orden.
Los franciscanos establecieron conventos y hospitales en lugares como la Ciudad de México, Puebla, Estado de México, Michoacán, Jalisco y Yucatán.
Los dominicos fueron la segunda orden en llegar a Nueva España en 1526, se ubicaron en las regiones del sur desde Oaxaca hasta Guatemala.
Años después, para 1533, llegaron los agustinos, ellos se establecieron en aquellas regiones no ocupadas por las otras órdenes religiosas, como el occidente, las Huastecas y el Pánuco, ahí abrieron conventos y orfanatos.
Más tarde, en 1572, llegó la Compañía de Jesús, también conocidos como jesuitas, quienes se dedicaron a establecer colegios en muchas ciudades, y un sistema de misiones en las regiones más alejadas del noroeste. Además, se consagraron a la educación de los criollos y a la enseñanza superior.
Seguro se estarán preguntando: ¿cómo lograron comunicarse los frailes con los indígenas? Pues bien, utilizaron todo tipo de recursos: elaboraron dibujos similares a los de los códices para escribir las oraciones y enseñanzas, decoraron los techos de las capillas con diferentes escenas religiosas, aprovecharon el gusto de los indígenas por el teatro y la música para recrear pasajes religiosos en pequeñas obras de teatro y realizaron fiestas con música y canto.
Ahora bien, es conveniente mencionar que llegaron a Nueva España dos tipos de religiosos: los que pertenecían al clero regular y los del clero secular.
En este triángulo les explico esta situación: el clero regular estaba constituido por las órdenes religiosas y obedecían directamente a Roma. El clero secular estaba formado por los sacerdotes, obispos, párrocos que no pertenecían a ninguna orden religiosa y se encontraban ligados a la sociedad civil.
Durante el proceso de evangelización, a los indígenas poco a poco les hicieron perder sus ritos dirigidos a los más de cien dioses que adoraban. Algunos indígenas aprendieron latín e incluso se volvieron frailes o sacerdotes. El catolicismo vino a cambiar el pensamiento religioso de los pueblos de Mesoamérica.
Ahora revisa: EL ÁMBITO SOCIAL
El ámbito social se refiere a la forma en que se organizan y relacionan las personas en un tiempo y espacio determinado.
La población originaria del México antiguo registró un drástico descenso demográfico en el siglo XVI, principalmente por la propagación de enfermedades como el sarampión y la viruela, las cuales eran desconocidas y, por tanto, la población originaria no tenía defensas para combatirlas.
Esta situación y la necesidad de poblar la naciente Nueva España fue lo que motivó la llegada de inmigrantes de diferentes partes del mundo, aunque las causas de la llegada de unos y otros obedeciera a diferentes intereses.
Los españoles y otros europeos fueron de los primeros inmigrantes que llegaron de manera voluntaria a Nueva España. Las leyendas sobre las grandes riquezas del Nuevo Mundo atrajeron a la población de Castilla y de otras regiones de España y de Europa.
Así, otro grupo de inmigrantes fueron los africanos. María Elisa Velázquez Gutiérrez, en su artículo “La raíz africana en México”, refiere que los primeros africanos llegaron con los exploradores y conquistadores de América, tal y como lo muestra el Códice Azcatitlan en la siguiente imagen.

https://www.noticonquista.unam.mx/imagen-popup/313
Los africanos fueron obligados a llegar a Nueva España, comprados como esclavos por autoridades españolas tanto civiles como religiosas, fundamentalmente para desempeñar labores domésticas. Al respecto, las fuentes históricas refieren que alrededor de 250 000 personas esclavizadas arribaron a Nueva España, sin contar las que llegaron de contrabando.
Un tercer grupo de población que migró (algunos de manera voluntaria y muchos más de manera forzada) a Nueva España fueron los asiáticos. Desde fechas tempranas, Nueva España mantuvo una relación importante con Asia, especialmente con las islas Filipinas.
Fue a través del Galeón de Manila como se propició la continua y compleja migración de asiáticos libres y esclavos entre los años 1565 y 1700.
Finalmente, otro sector de la población asiática que migró a Nueva España fueron los moros o musulmanes, quienes llegaban al puerto y se quedaban trabajando en Acapulco o se dirigían a la Ciudad de México. La condición para que esta comunidad pudiera permanecer en la Nueva España fue que renunciaran a su religión del Islam y se cristianizaran.
La presencia de personas europeas, africanas y asiáticas en la compleja sociedad novohispana originó no sólo el encuentro e intercambio cultural entre indígenas, africanos, asiáticos y españoles, sino que, con el tiempo, también generó el mestizaje étnico, así como las intenciones de los españoles por reforzar un sistema de estratificación social basado en el origen étnico a través de la denominación de las castas.
Hasta aquí el ámbito social.
El propósito de esta sesión fue: “Reconocer el proceso de conquista y colonización del México antiguo y el periodo fundacional de la Nueva España”. Como viste, los primeros años de la vida virreinal fueron diversos y dividirlos en sus ámbitos de estudio ayuda a analizar cada uno de una mejor forma. Conocerlos es conocer parte de nuestro pasado y nuestro presente, ya que muchas cosas de la cultura virreinal hoy se siguen practicando.
El reto de hoy:
Elabora un mapa conceptual con las principales características económicas, políticas, sociales y culturales de Nueva España en el siglo XVI.
Recuerda que en tu libro de texto puedes obtener más información sobre el tema. En tu casa seguramente tienes revistas, libros o tal vez un teléfono inteligente con el que puedes investigar más acerca de estos procesos históricos en Internet.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion