Las flotas, el control del comercio y el Consulado de Comerciantes
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:17
Las flotas, el control del comercio y el Consulado de Comerciantes
Aprendizaje esperado: explica la importancia del comercio y de la plata novohispana en el mundo.
Énfasis: analizar la actividad comercial de Nueva España y la formación del Consulado de Comerciantes.
¿Qué vamos a aprender?
Estudiarás el comercio de Nueva España con otras regiones del mundo. Verás que por los puertos de Veracruz y Acapulco ingresaban al territorio productos de regiones de ultramar nunca antes vistos y que, por ellos, también se envíaban los productos novohispanos como la plata, que alimentaba la circulación de moneda en todo el mundo
Se te recomienda tener a la mano una libreta y un bolígrafo para que hagas tus anotaciones, también puedes utilizar tu libro de texto para que consultes mapas, imágenes o los temas en particular.
¿Qué hacemos?
Observa la siguiente pintura que representa la gran variedad de productos que se comerciaban en la época virreinal.

Se trata de un “Puesto de Mercado”. ¿Qué productos conoces? ¿Qué personajes puedes distinguir?
Puedes observar diferentes frutas caramelizadas, verduras, plátanos colgados, cacahuates, cocos y pescados colgados que, seguramente, fueron especiados con productos provenientes de Asia.
Además, al fondo puedes identificar cestas elaboradas con fibras naturales, algunos jarrones de vidrio y ciertas botellas que, tal vez, contenían vino.
En la pintura también se aprecia a dos hombres decidiendo qué comprar y dos niños, que tal vez quieren probar alguna fruta.
Por último, observas a las dos vendedoras cargando un “huacal”, que posiblemente van a intercambiar. ¿Qué contendrá aquel paquete? ¿De qué región de Nueva España vendría? o ¿sería un producto de otro país?
Imagina por un momento que cerca de ese puesto venden jarrones de porcelana y telas exóticas provenientes de Asia; ropa, sombreros y vinos provenientes de Europa, es decir, diferentes productos de casi todo el mundo.
Por lo anterior, surgen las siguientes preguntas:
- ¿Cómo llegaban a Nueva España productos de lugares tan lejanos como de Europa o Asia?
- ¿Qué dificultades encontraban a su paso?
Una vez consolidado el proceso de conquista, los españoles fueron los primeros beneficiarios de las riquezas naturales y de la mano de obra de los indígenas.
Debes recordar que la encomienda fue la primera organización de trabajo en Nueva España y que, en su gran mayoría, se dedicó a explotar la tierra. No pasó mucho tiempo para que los españoles introdujeran nuevas actividades económicas como la ganadería y la minería.
También, debes tener claro que durante los siglos XVI y XVII la economía europea se basó en el sistema económico mercantilista que medía la riqueza de las naciones a partir de la plata y oro que acumulaban.
Además, en este sistema, el estado se hacía responsable de las políticas comerciales que mejor le conviniera a sus intereses, por lo que había un estricto control del estado a las operaciones comerciales.
En términos generales, España diseñó una ruta comercial cerrada y proteccionista para Nueva España con el fin de que no entrara nada ni nadie sin el consentimiento de la metrópoli. Para tal efecto, se creo el Consulado de Comerciantes de Sevilla quienes establecieron reglas muy estrictas acerca de qué productos y personas se trasladaban de España a América. Además, el consulado podía negar la licencia a un barco para cruzar por el Océano Atlántico.
De acuerdo con Bernardo García Martínez, en el libro, Nueva Historia General de México, el monopolio comercial de España sobre Nueva España tenía tres propósitos. El primero entorpecer o prohibir en tierras americanas la producción de bienes de consumo como herramientas de hierro, textiles finos, aceite, vino y papel, con el objeto de proteger a los manufactureros españoles. El segundo limitar o anular el comercio entre las colonias americanas, por ejemplo, entre Perú y México. El tercero condicionar el comercio trasatlántico a una vía exclusiva: el eje Veracruz-Sevilla.
Cómo puedes darte cuenta, el comercio novohispano estuvo muy controlado. A esta situación se sumaba el problema de los piratas.
Lee el siguiente texto que refiere el robo comandado por un pirata francés a tres barcos comerciales proveniente de Nueva España con destino a la Metrópoli, y la sorpresa que se llevó.
El relato se titula Corsarios. El asalto a los galeones españoles, y pertenece a Xabier Armendáriz
En la primavera de 1522, el francés Jean Florin, conocido por los españoles como Juan Florín o el Florentino, mandaba una flotilla de barcos piratas que patrullaban las islas Azores en busca de presas […]
Una mañana avistó tres carabelas en el horizonte. Intentó rendir las naves con disparos de advertencia, procurando causar el menor daño para no hundirlas y poder tomarlas al abordaje. Inmediatamente lanzó sus barcos contra dos de ellas, sin percatarse de que una tercera huyó, refugiándose en la isla de Santa María.
Días más tarde, la carabela, creyendo segura la navegación, zarpó hacia la Península escoltada por varias naves al mando de Domingo Alonso. Sin embargo, Florín y sus hombres continuaban allí y dieron caza a la carabela y su escolta, hasta que lograron capturarlas a la altura del cabo San Vicente, al sur de Portugal.
Cuando el pirata subió a bordo su sorpresa fue mayúscula. No se trataba de una mera carabela mercante, sino que transportaba el fabuloso tesoro robado por Hernán Cortes al emperador azteca Moctezuma tras la conquista de Tenochtitlán.
Según el cronista Bernal Díaz del Castillo: «Ochenta y ocho mil castellanos en barras de oro […] fueron muchas joyas muy ricas y perlas, tamañas algunas como avellanas, y muchos chalchiuíes, que son piedras finas como esmeraldas y aún una de ellas tan ancha como la mano».
En total, Florin se hizo con 58.000 barras de oro y el tesoro personal del emperador azteca, que incluía su famoso penacho de plumas. Por si fuera poco, se apoderó de otro barco proveniente de Santo Domingo, añadiendo 20.000 pesos en oro y perlas al botín.
La acción de Juan Florín tuvo la virtud de abrir los ojos a las naciones europeas, que tomaron conciencia de las riquezas del Nuevo Mundo. En pocos años, las costas americanas se vieron inundadas de corsarios y piratas, unos intentando resarcir a sus reyes del monopolio español y portugués, otros trabajando por cuenta propia. Dejaban pasar a los mercantes a la ida, para asaltarlos a la vuelta cargados de riquezas. Con el incremento de las capturas se apoderaron también de las cartas con las rutas de navegación, y desde entonces los ladrones del mar ya supieron dónde buscar.
Ante la amenaza de los piratas, pronto se hizo patente la necesidad de un sistema de convoy con escoltas. Desde los puertos de Veracruz, México; Portobelo, Panamá, y Cartagena de Indias, Colombia, entre otros, las riquezas americanas eran enviadas mediante flotas fuertemente custodiadas a La Habana, en Cuba. Alrededor de junio, la Flota de Indias o del Tesoro zarpaba de esta isla escoltada en vanguardia por la nao capitana, a retaguardia por la almiranta y a un costado por los galeones de barlovento.
De este modo, las carracas y naos mercantes quedaban a salvo de los ataques, mientras que la mayor parte del oro y la plata se transportaban en las bodegas de galeones fuertemente artillados. En estas condiciones las reglas del juego cambiaron, y la Flota de Indias sólo fue capturada en dos ocasiones: por el holandés Piet Heyn en 1628, y por los ingleses Blake y Stayner en 1657.
La lectura resulta intreresante; pero también es significativa porque, a partir de este acontecimiento, la piratería financiada por potencias coloniales rediseñó su estrategia para apoderarse de la riqueza de los Imperios enemigos. Por otro lado, las potencias coloniales también diseñaron una extrategia para proteger los recursos extraídos de sus colonias. Así, España instauró la Armada de Barlovento, además de nuevas rutas marítimas para evitar que sus riquezas fueran capturadas por los piratas.
Para profundizar sobre los piratas observa el siguiente video titulado “Al abordaje”.
- Al abordaje
https://www.youtube.com/watch?v=XuFv8ziwOqI
Mucha plata, oro y productos de otras culturas fueron a parar a Francia, Inglaterra u Holanda debido a la piratería promovida por estas potencias; y los piratas que lo hicieron posible fueron premiados por su “valentía”.
Los piratas fueron un dolor de cabeza para la Corona española pues atacaron puertos en el Mar Caribe, del actual territorio nacional, de donde zarpaban las riquezas para la metrópoli.
Para evitar ser asaltados por piratas, se construyeron fuertes en diferentes puertos como en Campeche y en La Habana, Cuba.
Debes tener claro que la piratería no fue una práctica exclusiva de Inglaterra, sino que también Francia y Holanda promovieron esta actividad. Además, algunos piratas eran independientes de las potencias, y lo que robaban, en ocasiones, lo revendían a las colonias españolas.
Para proteger al comercio español y novohispano se estableció un sistema de flotas en 1543, conformado por naves comerciales que viajaban juntas y eran resguardadas por dos barcos de Guerra, es decir, como una especie de guardaespaldas o policía marítima.
En muchas ocasiones, los barcos comerciales trasladaban inmensas cantidades de plata a España proveniente de Perú o de Nueva España, por esa razón esos barcos eran codiciados por los piratas o corsarios ingleses, franceses y holandeses.
Analiza las dos imágenes siguientes:
En este grabado ¿Qué puedes observar? ¿Qué puedes distinguir?


Se trata del puerto de Sevilla en España. Recuerda que la ruta comercial más importante de Nueva España durante el siglo XVI fue la de Veracruz-Sevilla.
En el grabado puedes identificar dos barcos que se acercan a la costa, hay cargadores, pequeños barcos y faros rústicos que tal vez funcionaban, también, como almacenes.
Cada año partían de Sevilla dos barcos con destino al Puerto de Veracruz, a la flotilla se le denominó Flota de Nueva España. De puerto a puerto, el viaje de ida duraba tres meses, y de regreso, el trayecto era un poco más tardado, de cuatro a siete meses, ya que las embarcaciones iban más al norte para evitar los vientos alisios.
En la segunda imagen, del Códice Florentino, se observa desembarcar en el Puerto de Veracruz a los españoles cargados de diferentes mercancías e incluso animales que no existían en América como cabras, cerdos, vacas y caballos. Además, puedes ver a indígenas observando a los barcos españoles que se acercan a la costa.
Un contrapeso del comercio del eje Veracruz- Sevilla fue el intercambio con las Filipinas. Ten presente que España conquistó aquel archipiélago en 1565 y estableció el contacto marítimo regular de Acapulco a Manila. Es decir, Nueva España contó con dos rutas comerciales marítimas: una por el Océano Atlántico; la otra por el Océano Pacífico.
El galeón de Manila, mejor conocido como Nao de China, hacía la ruta Manila-Acapulco y traía diferentes mercancías de mucho valor. Galeón es un tipo de barco especializado para la guerra o para el comercio.
Cuando los galeones de Manila llegaban a Acapulco se hacía una feria para vender los productos exóticos de aquellos lugares distantes, de culturas diferentes a la americana y europea.
La feria de Acapulco duraba cerca de un mes y se podían encontrar desde especias hasta grandes muebles para la decoración de una casa.
Los productos que más apreciaban los asiáticos, provenientes de Nueva España, sin lugar a dudas, era la plata, ya que en Asia era escaso ese metal, pero no debemos olvidar que también se enviaba vainilla y tabaco.
Observa el siguiente mapa:
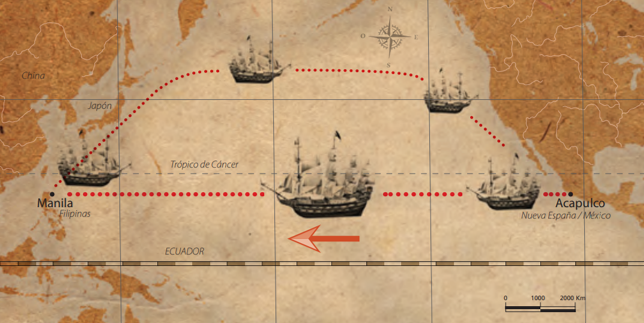
Como puedes apreciar, la ruta de Acapulco a Manila se hacía por el Océano Pacifico. Recuerda que el transcurso de ida podía tardar hasta tres meses y el de regreso podía tardar hasta siete meses, ya que los barcos debían irse por el norte para evitar los vientos alisios.
Los galeones que salían de Acapulco tenían que llegar a las islas Marianas y de ahí se iban a un largo viaje que podía ser muy difícil por las tormentas o los vientos fuertes.
Además, esta ruta, como la del Atlántico, podía ser atacada por los piratas ingleses, franceses u holandeses ya que, se sabía, muchas de las embarcaciones iban muy cargadas de productos asiáticos o de plata novohispana. El primer viaje a Manila se realizó en 1573 y el último en 1821.
Has revisado las dos únicas rutas comerciales que tenía Nueva España con Europa y Asia, pero ¿qué productos intercambiaban los españoles y los novohispanos?, ¿qué productos intercambiaban los asiáticos y los novohispanos?
Según Agustín Cue Canovas, de España se traían:
- Vino
- Aceite
- Lencería
- Vajilla
- Jarcias
- Papel
- Objetos de hierro
- Vinagre
- Aguardiente
- Jabón
De Asia se traían:
- Seda cruda, floja y torcida
- Tejidos de seda
- Telas finas de algodón
- Almizcle
- Ámbar
- Incienso para uso religioso
- Perlas
- Muebles finos
- Marfiles
- Porcelana china
De Nueva España se llevaban a España y Asia:
- Plata
- Oro
- Grana cochinilla
- Cueros
- Azúcar
- Vainilla
- Tabaco
- Cacao
Todos estos productos, pueden resultar asequibles y fáciles de encontrar, pero hace cinco siglos comprar o localizarlos era difícil y costoso, sobre todo si las mercancias provenían de Asia o Europa.
Para acaparar los productos que producía Nueva España y los que se importaban, los comerciantes novohispanos conformaron en 1594 el Consulado de Comerciantes de la Ciudad de México, institución donde se podía deliberar si un comerciante era desleal o no a los intereses económicos de la Corona española.
El Consulado lo integraban comerciantes mayoristas peninsulares que comerciaban a larga distancia de la Ciudad de México a otras ciudades importantes del actual territorio nacional. Algunos tenían influencia en los dos principales puertos: Veracruz y Acapulco.
Por su condición de españoles, conocían a otros comerciantes de Sevilla e incluso de Manila. Por estas razones, el poder económico de algunos comerciantes novohispanos fue muy grande. Puedes mencionar el nombre de Pedro Romero de Terreros, fundador del Monte de Piedad, dueño de diferentes minas.
Dice un comentario de la época que la cantidad de plata de ese hombre era tal que podía fácilmente construir un puente de Veracruz a Sevilla de ese metal tan preciado.
Al inicio de la sesión se formularon las siguientes preguntas: ¿Cómo llegaban a Nueva España productos de lugares tan lejanos como de Europa o Asia?, y ¿Qué dificultades encontraban a su paso?
Puedes concluir que Nueva España encontró en su metrópoli, España, un freno para desarrollarse económicamente, con la imposición de reglas duras para no comerciar directamente con naciones europeas e incluso ni con otras colonias. Así, sólo dos rutas se autorizaron para el comercio: la de Veracruz- Sevilla y la de Acapulco-Manila.
Con esas dos rutas marítimas, una por el Atlántico y otra por el Pacífico, lograron cubrir la demanda de productos traídos de otros continentes. El traslado de las mercancías de un continente a otro fue aprovechado por los piratas quienes robaban los barcos españoles y las riquezas eran trasladadas al país de origen del pirata: Inglaterra, Francia u Holanda.
Recuerda que en Nueva España los comerciantes más poderosos se organizaron en el Consulado de Comerciantes donde deliberaban asuntos comerciales internos y externos a la Colonia; y sus influencias llegaban hasta Sevilla o hasta Manila.
El reto de hoy:
Realiza en tu libreta un cuadro de doble entrada, en una columna escribe los productos que Nueva España enviaba a Europa y Asia, y en la segunda columna, las mercancías que llegaban de Manila y Sevilla.
Elabora dos bitácoras de viaje, imagina que son comerciantes novohispanos que viajan de Veracruz a Sevilla y de regreso, además, que realizan otro viaje comercial pero ahora de Acapulco a Manila ¿Qué tipo de producto venderías en cada continente? ¿Cómo sería tu viaje en los galeones? ¿Qué productos los sorprenderían más en Sevilla y en Manila? ¿Cuál sería la reacción de los novohispanos al ver nuevos productos de otros continentes? Utiliza colores, imágenes o revistas para ilustrar.
Recuerda que en tu libro de texto puedes obtener más información sobre el tema; en tu casa, seguramente tienes revistas, libros o, tal vez, un teléfono inteligente con el que puedas investigar más acerca de este proceso histórico en internet.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:










Login to join the discussion