Recordando el México antiguo II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:16
Aprendizaje esperado : reconoce características políticas, económicas, sociales y culturales del México antiguo.
Énfasis : reconocer la organización política, económica, social y cultural del México antiguo.
¿Qué vamos aprender?
Repasarás temas que tienen que ver con la historia del México antiguo.
Continuarás con el recorrido de las características sociales, culturales, económicas y políticas de Mesoamérica.
En la sesión anterior repasaste los temas relativos a las superáreas y los horizontes culturales de Mesoamérica, ahora revisarás las principales expresiones culturales, las formas de gobierno, las actividades económicas y la estructura de las sociedades mesoamericanas.
El repaso lo harás jugando un crucigrama virtual, así que asegúrate de mencionar la respuesta correcta para que lo vayas completando.
¿Qué hacemos?
Lee la siguiente e interesante lectura titulada “La alimentación en el México prehispánico”, del libro Historia General de México. Esta lectura ilustra la comida. Reflexiona: ¿qué comían los antiguos mexicanos?, ¿todos se alimentaban igual?
Los pueblos mesoamericanos cultivaron una gran diversidad de plantas comestibles, cercana a 190 especies diferentes que conjuntamente con plantas y frutas silvestres, más animales domésticos o salvajes formaron la base de una de las dietas más ricas del mundo.
La dieta común estaba compuesta por tortillas, atole, tamales, frijoles, granos de amaranto y agua de chía como bebida; algunas veces comían carne de venado o de guajolote.
Generalmente se comía solamente dos veces al día. El atole y el chocolate endulzados con miel de maguey o miel de abejas silvestres y aromatizados con vainilla, anís u otras plantas eran las bebidas más apreciadas por los mesoamericanos.
Para los gobernantes y sacerdotes había numerosos platillos: guajolote, faisán, pato, venado, pichón, liebre y conejos, pescado y frutas variadas. Acostumbraban comer los tamales rellenos de carne, caldo de ave, ranas con salsa de chile, pescado con tomate o con salsa de pepitas de calabaza molidas, axolotl sazonado con chile amarillo, gusanos de maguey asados, atole endulzado y raíces como el camote.
La tortilla, una torta plana de harina de maíz, se convirtió en la dieta de los pueblos mesoamericanos. La mujer dedicaba gran parte de su tiempo en la preparación de ellas. Por la tarde ponía el nixtamal –maíz húmedo con cal- en una cazuela de barro. Al amanecer y auxiliada con la piedra plana para moler, el metate y la mano de piedra, el metlapil, molía el nixtamal para obtener la masa de la cual tomaba porciones que palmeaba hasta formar la tortilla.
[…]
Una planta de uso típicamente mesoamericano era el cacao, de cultivo restringido geográficamente a zonas calientes y húmedas que antiguamente tenía una difusión mucho mayor debido al uso de riego en regiones áridas como la cuenca de Balsas. La vainilla para perfumar la bebida de cacao es fruto de una orquídea cultivada en la selva tropical. Probablemente conocidas, aunque de importancia limitada, eran dos plantas hoy mucho más usadas: el cacahuate (tlalcacahuatl) y la piña (matzatli).
¿Te percataste que los gobernantes y sacerdotes tenían una dieta más variada que el resto de la población? No obstante, en realidad la base de la dieta mesoamericana era la misma: el maíz.
Recordarás que en Mesoamérica la sociedad estaba claramente estratificada.
Analiza la siguiente imagen.
¿Puedes reconocer qué es lo que representa?

Esta imagen representa la pirámide social de los mexicas. Se trataba de una sociedad cuya jerarquía estaba muy bien delimitada y en la que cada miembro desempeñaba tareas propias de su clase. En la cúspide de la pirámide encontramos a los Pipiltin encabezada por el Tlatoani; le seguían los sacerdotes, la nobleza y los guerreros; continuaban los macehuales y en la base se encontraban los esclavos.
También recuerda que las culturas mesoamericanas no sólo tenían bien delimitada su estructura social. Sino también compartían otros rasgos muy característicos, como la religión y cosmovisión, que fueron de mucha importancia, pues su influencia estaba presente en todos los aspectos de la vida cotidiana.
¿Qué representa la siguiente imagen?
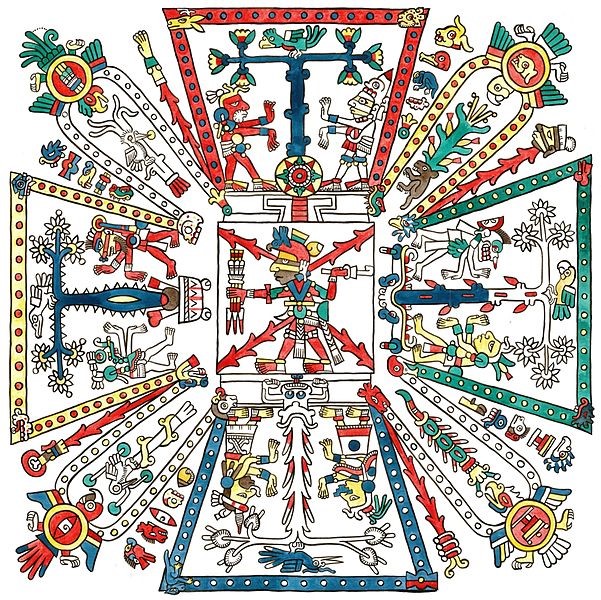
La imagen pertenece a la primera página del Códice Féjérvary-Mayer, también llamado Pochteca y este códice representa la cosmovisión y bases de la religión mesoamericana. En el códice puedes observar que concebían al mundo dividido en cuatro puntos cardinales asociados a un dios y al centro del universo la tierra.
Analiza la siguiente imagen y responde:
¿Qué actividad representa?

Este detalle del códice Florentino representa una de las principales actividades económicas de Mesoamérica, se refiere a la agricultura, pues la subsistencia de su población dependía en gran parte de esta actividad, principalmente del cultivo de maíz, frijol y chile.
¿Podrías decir qué tipo de escultura es la que se muestra en la siguiente imagen?

El tipo de escultura que muestra la imagen es la monolítica, es decir, se trata de una escultura realizada sobre una enorme roca. En la imagen, concretamente identificas una gran cabeza olmeca que según se cree, representaba a uno de sus gobernantes.
Para recordar de mejor manera, observa el siguiente video. Toma particular atención a las características sociales de cada horizonte cultural.
-
Primeros centros urbanos mesoamericanos
https://www.youtube.com/watch?v=LsvSYLc3hUc
Seguramente te ayudó a recordar las características culturales de Mesoamérica.
Ahora comenzarás tu juego de crucigrama, se te plantearán preguntas y tu deberás intentar responder.
Comienza por la primera pregunta horizontal:
1. ¿Cuál era la principal actividad económica de las culturas mesoamericanas?
La palabra es AGRICULTURA. Pues fue la principal actividad económica de las culturas mesoamericanas, específicamente con la siembra de maíz, frijol y chile, que eran la base de la alimentación.
Es correcto, continúa con la segunda palabra horizontal:
2. Eran grandes construcciones que servían como centros ceremoniales alrededor de las cuales se establecían ciudades.
La palabra que buscamos es: PIRÁMIDES. En el aspecto arquitectónico, en Mesoamérica se construyeron grandes basamentos piramidales y dieron a sus ciudades un trazo semejante al de una cruz, con cuatro calzadas que representaban los cuatro rumbos del universo.
Ahora la tercera palabra horizontal:
3. ¿Cuál es el tipo de religión que se practicaba en Mesoamérica, que consistía en la creencia en varios dioses?
La palabra es: POLITEÍSTA.
Las culturas mesoamericanas tuvieron una religión de carácter politeísta, es decir, creían en dos o más deidades. Poseían la idea de un tiempo cíclico, pues creían que las características presentadas en ciertos periodos se repetirían en el futuro. La misión de los humanos consistía en alimentar con sangre a los dioses para que los ciclos continuaran. Por eso muchos pueblos practicaban el sacrificio humano.
Ahora, continua con las verticales.
En las culturas mesoamericanas, existían dos tipos de calendarios. La primera pregunta es:
1 ¿Cuál era el calendario que regía la fecha de las cosechas?
La palabra correcta es: SOLAR. En relación con la astronomía, los mesoamericanos tenían dos calendarios, entre ellos el solar. Este calendario regulaba la fecha de las cosechas y constaba de 360 días, más cinco días vacíos.
el calendario solar establecía las fechas en que se llevarían a cabo las cosechas. Por otra parte, con el calendario ritual, los sacerdotes podían interpretar algunos sueños y establecer días festivos.
Continua con la segunda palabra vertical.
2. ¿Cómo se le conoce actualmente a una ceremonia en forma de juego que representaba la regeneración de la vida y simbolizaba el comienzo y fin de los ciclos?
Es JUEGO DE PELOTA, pues este juego era uno de los rituales más importantes para las civilizaciones mesoamericanas. Aunque en apariencia se trataba solamente de un deporte, su importancia iba más allá de entretener a los asistentes, pues a través de esa ceremonia, las culturas de la región interpretaban la regeneración de la vida, el cierre y comienzo de nuevos ciclos y la lucha entre el bien y el mal, la claridad y la oscuridad.
Tu crucigrama ya casi está completo, solamente hace falta la tercera palabra vertical.
3. Su significado en español quiere decir “el orador” o “el que habla”. Para la cultura mexica, era su máxima autoridad política, es decir, el máximo gobernante.
La respuesta es TLATOANI, o como también le conocían los mexicas: “huey Tlatoani”, quien era la máxima autoridad y desempeñaba funciones religiosas y militares, además de las tareas políticas y sociales propias de la nobleza.
Observa el siguiente video acerca de la importancia que para las culturas del México antiguo tenía el registro del tiempo y la relación que consideraban guardaba con el ciclo de la vida, entendida en un sentido amplio.
-
Piedra del Sol o calendario Azteca
https://www.youtube.com/watch?v=e8k2G4wcPhs
En síntesis, puedes afirmar que las expresiones culturales del México antiguo, entre otras, fueron: la construcción y planeación de centros ceremoniales y basamentos piramidales, el juego de pelota, el uso del calendario, y la práctica del sacrificio humano en sus rituales.
Lo interesante es que casi todas ellas estaban vinculadas con la religión politeísta.
Por otra parte, debes recordar que, dentro del ámbito económico, la agricultura tuvo un lugar importantísimo para las culturas mesoamericanas, pues de esta actividad dependía la subsistencia de sus habitantes. Por tanto, el maíz, el frijol y el chile fueron esenciales no sólo para la economía, sino para su propia alimentación y el intercambio de bienes de primera necesidad que se efectuaba principalmente a través del trueque.
Por otra parte, en la esfera política y social, no debes olvidar que las sociedades mesoamericanas tenían una jerarquía bien establecida, donde en lo más alto de la pirámide social se encontraban los nobles o pipiltin, pasando por los macehualtin que eran personas comunes del pueblo y, por último, los esclavos que ocupaban el nivel más bajo de la sociedad.
El reto de hoy:
En tu libreta elige el tema del México antiguo que más te haya gustado y elabora un crucigrama como el que acabas de realizar, e intenta resolverlo con tus familiares.
Para superar el reto y ampliar más tu conocimiento sobre lo que aprendiste el día de hoy, puedes consultar el libro de texto de tercer grado de secundaria o pedir apoyo a tus maestros.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/secundaria.html











Login to join the discussion