La evangelización en Nueva España
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:16Aprendizaje esperado: Analiza las consecuencias de la conquista y la colonización española.
Énfasis: Analizar el proceso de evangelización en Nueva España.
¿Qué vamos a aprender?
Recordarás que la Historia es la memoria de los pueblos, y su conocimiento te ayudará a saber cómo era antes, cómo se ha transformado y cómo es ahora nuestro país.
Por ello, a lo largo de esta sesión analizarás las consecuencias de la conquista y la colonización española, específicamente, la evangelización en Nueva España.
Te has preguntado, ¿cómo fue el proceso de evangelización? y ¿cuál es su herencia cultural?
Es evidente que la conquista de Tenochtitlan fue el parteaguas para la apertura de nuevas costumbres y tradiciones. Además, sentó las bases para el nacimiento del virreinato de Nueva España.
El propósito es analizar el proceso de evangelización en Nueva España. Por tanto, conocerás quiénes se encargaron de llevar a cabo la predicación, enseñanza e implementación de la fe católica en los territorios de Nueva España.
Además, revisarás la labor de algunos misioneros que se caracterizaron por denunciar los abusos cometidos por los españoles y ser considerados símbolos de protección para los indígenas.
Así que, descubre lo relacionado con la tarea evangelizadora, herencia de la época colonial.
Realiza anotaciones por si deseas profundizar y ampliar tus conocimientos acerca del tema en cuestión.
¿Qué hacemos?
Lee los siguientes dos textos conservados en castellano, el primero recogido por Jerónimo de Mendieta, y el segundo por Bernal Diaz del Castillo en su libro Historia verdadera de la Conquista de la Nueva España .
Primero el testimonio de Mendieta:
Y mientras estos religiosos caminaban para México [...], los
indios se andaban tras ellos como los muchachos suelen
seguir a los que causan novedad, y maravillándose de verlos
con tan desarrapado traje, tan diferente de la bizarría
y gallardía que en los soldados españoles antes habían visto.
Y decían unos a otros, ¿Qué hombres son estos tan pobres?
¿Qué manera de ropa es esta que tráen?
No son estos como los otros cristianos de Castilla, y menudeaban mucho un vocablo suyo diciendo: motolinía, motolinía.
Y uno de los padres, llamado fray Toribio de Benavente, preguntó a un español que qué quería decir aquel vocablo que tanto lo repetían.
Respondió el español: padre, motolinía, quiere decir pobre o pobres.
Entonces dijo fray Toribio, ese será mi nombre para toda la vida y así de allí adelante nunca se nombró ni firmó sino fray Toribio Motolinía.
Ahora el testimonio de Bernal Diaz del Castillo:
Después de quitadas las idolatrías y todos los malos vicios que usaban […] se han bautizado desde que lo conquistamos todas cuantas personas había, ansí hombres como mujeres e niños que después han nacido, y que de antes iban perdidas sus ánimas a los infiernos y agora, como hay muchos y buenos religiosos de señor San Francisco y de Santo Domingo y de otras órdenes, andan en los pueblos predicando, y en siendo la criatura de los días que manda nuestra santa madre iglesia de Roma los bautizan; y demás desto con los santos sermones que les hacen el santo Evangelio está muy bien plantado en sus corazones, y se confiesan cada año, y algunos dellos que tienen más conocimiento en nuestra fe se comulgan; y demás desto tienen sus iglesias muy ricamente adornadas de altares, y todo lo perteneciente para el santo culto divino, con cruces y candeleros y ciariales y cáliz y patenas y platos, unos grandes y otros chicos, de plata, y incensario, todo labrado de plata; pues capas y casullas y frontales en pueblos ricos los tienen, y comúnmente, en razonables pueblos, de terciopelo y de damasco y raso y de tafetán, diferenciados en los colores y labores, y las mangas de las cruces muy labradas de oro y seda […]
Otra cosa buena tienen: que así hombres como mujeres y niños que son de edad para lo deprender, saben todas las santas oraciones en sus mismas lenguas que son obligados a saber, y tienen otras buenas costumbres acerca de sus santa cristiandad, que cuando pasan cabe un santo altar o cruz abajan la cabeza con humildad, se hincan de rodillas y dicen la operación del “Pater noster” que les mostramos los conquistadores […].
Quizá hubo algunas palabras que nunca habías escuchado, te sugerimos indagar su significado.
El que no hayas escuchado antes las palabras, puede obedecer a que se trata de un castellano antiguo, por tanto, algunos términos están en desuso o han cambiado su redacción o significado.
El lenguaje se compara con un ser vivo, hay palabras de nueva creación, como si nacieran; hay palabras que se conservan por mucho tiempo, por lo mismo, un gran número de personas las conocen y utilizan, como si las palabras maduraran y crecieran; y también, hay palabras que se dejan de usar, como si desaparecieran o murieran.
Regresando a los testimonios que leíste, te percataste que comparten mucha información. La primera relacionada con las impresiones de sorpresa generada en algunos indígenas al contemplar el comportamiento de los primeros franciscanos en Nueva España. La segunda, refiere la percepción de un conquistador ante el proceso de evangelización de los indígenas.
Imagina ¿cómo crees que los religiosos católicos trataban a los indígenas? ¿Cuál consideras que era la reacción de los indígenas cuando los frailes se referían a sus antiguos dioses cómo demonios?
Observa las siguientes imágenes e intenta responder a las preguntas.

- ¿Cuántas personas identificas en el mural?
- ¿Cómo están vestidos?
- ¿Qué supones que están haciendo?
- ¿Qué objetos puedes identificar en la imagen?

- ¿Quiénes están ahí?
- ¿Qué actitud muestran?
- ¿Qué objetos observas?
- ¿Qué crees que represente la imagen?

- ¿Quiénes están ahí?
- ¿Qué actitud muestran?
- ¿Qué objetos observas?
- ¿Qué crees que represente la imagen?

- ¿Qué observas en las imágenes?
- ¿Qué crees que representen?
- ¿Cuál crees que haya sido el uso que le dieron?
- ¿Qué creen que represente la imagen?
- ¿Qué tipo de construcciones observan?
- ¿Cuál creen que haya sido el propósito de dichas construcciones?
Tras la caída de la gran Tenochtitlan el ejército vencedor, encabezado por Cortés y los españoles, ocupó el lugar que los mexicas tenían en el liderazgo mesoamericano.
Para muchos pueblos de la región no resultó extraño entregar tributos a los nuevos conquistadores, pues ya lo pagaban a los integrantes de la Triple Alianza.
Ante el sometimiento español, la mayoría de los indígenas fueron obligados a renunciar tanto a la veneración de sus dioses como a la realización de ceremonias rituales, esto posiblemente les resultó más complicado, por tanto, los conquistadores emplearon prácticas violentas e incluso sangrientas.
Algunos otros pueblos, principalmente inconformes con los mexicas, decidieron aliarse con los españoles, esto implicaba la sumisión al rey de España y la aceptación del cristianismo como religión única y verdadera.
Para conocer un poco más acerca del proceso de conquista espiritual, observa el siguiente video:
- Evangelización y manuscritos en lenguas indígenas
https://www.youtube.com/watch?v=nAQutfbpps4
La evangelización fue una forma de consolidar el dominio de la Corona española, a través de la tradición católica. Aunque la labor de los frailes no resultó nada fácil.
Después de que los españoles conquistaron México Tenochtitlan, Cortés solicitó al rey que enviara frailes para enseñar el cristianismo a los indígenas.
Los frailes tendrían la misión de evangelizar y erradicar las prácticas religiosas prehispánicas: franciscanos, dominicos, agustinos y más tarde, los jesuitas, fueron los religiosos que se dieron cita en la Colonia.
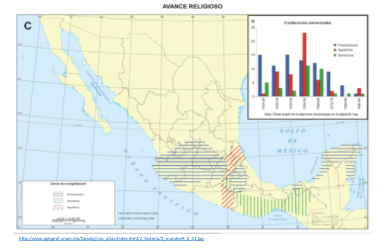
En 1523 llegaron a Nueva España los primeros tres frailes franciscanos. Un año más tarde, en 1524, arribaron doce más de esta misma orden.
Ellos consideraban que el descubrimiento de otros pueblos era un presagio de la cercanía del fin del mundo y que, por lo mismo, la conversión al cristianismo debía llevarse a cabo con celeridad, es decir, con mucha prisa.
Por ello, los franciscanos establecieron conventos y hospitales en lugares como la Ciudad de México, Puebla, Estado de México, Michoacán, Jalisco y Yucatán.
Un ejemplo es el convento de Santiago Tlatelolco, en la Ciudad de México. En este convento franciscano, Fray Bernardino de Sahagún fundó la escuela de Santa Cruz Tlatelolco en el siglo XVI.
Los dominicos fueron la segunda orden en llegar a Nueva España en 1526, se ubicaron en las regiones del sur, desde Oaxaca hasta Guatemala. Estos fundaron conventos y escuelas de oficios en el Estado de México, Puebla y Oaxaca, principalmente.
De gran importancia fue también la labor del dominico fray Bartolomé de las Casas, pues a través de sus obras y escritos se convirtió en el gran defensor de los indígenas ante los abusos de los conquistadores y colonizadores.
Años después, para 1533, llegaron los agustinos, ellos se establecieron en aquellas regiones no ocupadas por las otras órdenes religiosas, como el Occidente, las huastecas y el Pánuco, ahí abrieron conventos y orfanatos.
Entre los agustinos más destacados, podemos mencionar a fray Alonso de la Veracruz, pues denunció la injusticia de la conquista, además de ser el fundador en Tiripitío, Michoacán, del primer Colegio de Altos Estudios en América, al que acudieron tanto españoles como indígenas.
Más tarde, en 1572, llegó la Compañía de Jesús, también conocidos como jesuitas, quienes se dedicaron a establecer colegios en muchas ciudades y un sistema de misiones en las regiones más alejadas del noroeste. Además, se consagraron a la educación de los criollos y a la enseñanza superior.
Esta sucesión de las órdenes evangelizadoras no hubiera sido posible sin la participación de los colaboradores indígenas. Para conocer más de ello, observa el siguiente video:
2. Los colaboradores de los frailes
https://www.youtube.com/watch?v=d_0oduIa9fg&feature=youtu.be
Sin duda, gran parte de los documentos, tanto impresos como manuscritos, hubieran sido imposibles de redactar sin el conocimiento de los hablantes nativos.
Pero ¿cómo lograron comunicarse los frailes con los indígenas?
Pues bien, utilizaron todo tipo de recursos: elaboraron dibujos similares a los de los códices para escribir las oraciones y enseñanzas; decoraron los techos de las capillas con diferentes escenas religiosas; aprovecharon el gusto de los indígenas por el teatro y la música para recrear pasajes religiosos en pequeñas obras de teatro, y realizaron fiestas con música y canto.
Ahora bien, es conveniente mencionar que llegaron a Nueva España dos tipos de religiosos: los que pertenecían al clero regular y los del clero secular.
El clero regular estaba constituido por las órdenes religiosas, ya mencionadas anteriormente, y obedecían directamente a Roma.
El clero secular estaba formado por los sacerdotes, obispos, párrocos, que no pertenecían a ninguna orden religiosa y se encontraban ligados a la sociedad civil.
En general, los frailes fueron personas comprometidas con la defensa del indígena, aunque también había intereses políticos y económicos en las órdenes.
Entre los frailes más destacados de este periodo se puede mencionar a fray Toribio de Benavente, mejor conocido como Motolinía, seguro recuerdas por qué lo llamaban así, pues se mencionó en la primera lectura; fray Juan de Zumárraga, primer obispo de Nueva España, y fray Bernardino de Sahagún, quien dejó uno de los más importantes testimonios de la historia, costumbres y tradiciones de los indígenas en su obra Historia General de las Cosas de Nueva España , una de cuyas versiones es conocida como el Códice Florentino , elaborado en el colegio de Santa Cruz Tlatelolco.
Cómo pudiste darte cuenta, la conversión de los indígenas al cristianismo no sólo significó que los frailes les enseñaran el catecismo y las principales creencias de la religión cristiana.
El proceso de evangelización también supuso la transformación de muchas costumbres cotidianas, como fue, entre otras, la implantación del matrimonio cristiano y que los indígenas empezaran a cubrir ciertas partes de su cuerpo con ropa.
Además, durante este proceso, los frailes enseñaron a los indígenas a hablar castellano y, algunos de ellos, latín; a fabricar instrumentos musicales occidentales, a cantar en los coros de las iglesias, a participar en las fiestas de los santos, ir a misa y practicar los sacramentos.
El Reto de Hoy:
En una breve historieta, de sólo cuatro viñetas, intenta explicar el proceso de evangelización en Nueva España, recuerda que puedes utilizar imágenes, dibujos, textos breves y, por supuesto, onomatopeyas.
Las onomatopeyas son los sonidos naturales o provocados que se escriben y evocan a qué o quién los provoca.
Ejemplo de los primeros serían, el característico chipi-chipi de la lluvia; el gua-gua , o sea, el ladrido del perro o demás sonidos emitidos por ciertos animales, entre otros. Como ejemplo de los sonidos provocados serían el plash ; punch , zas , que evocan caídas, contactos, separación o golpes de objetos o personas.
Para superar el reto y ampliar más tus conocimientos puedes consultar el libro de texto de Tercer Grado de Secundaria y pedir apoyo a tus maestros.
Descarga tu clase dando clic
¡Buen trabajo!
Gracias por tu esfuerzo.






Login to join the discussion