Derechos sexuales de los jóvenes
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:15Aprendizaje esperado: ejercer sus derechos sexuales reproductivos de manera responsable e informada, y emplea recursos personales para establecer relaciones de pareja o noviazgo, sanas y placenteras.
Énfasis: salud integral. Ejercer sus derechos sexuales de manera responsable e informada.
¿Qué vamos a aprender?
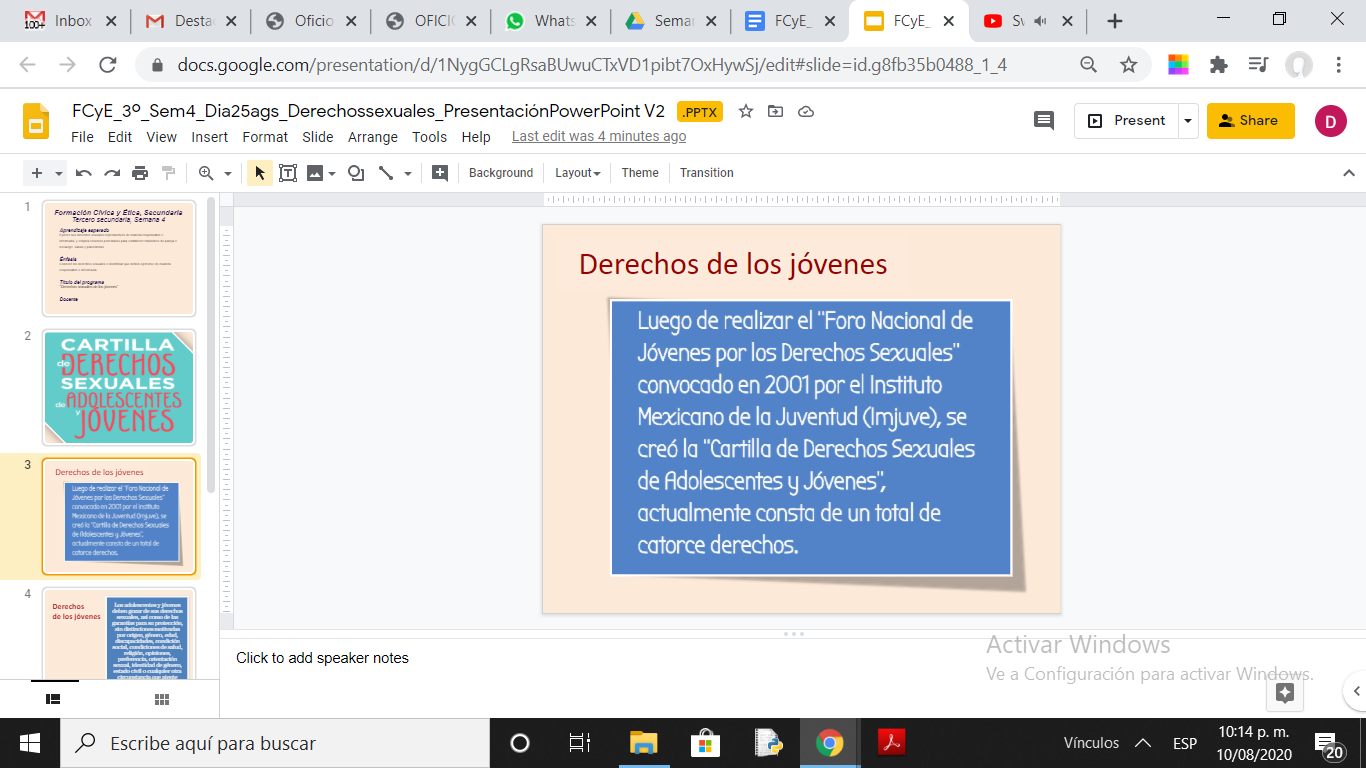
El ejercicio y garantía de los derechos sexuales de los jóvenes en México y el mundo en general, son sumamente importantes en la actualidad. En nuestro país, existe la Cartilla de derechos sexuales de adolescentes y jóvenes.

La primera pregunta es, ¿por qué surge esta cartilla?, ¿en qué contexto se genera un marco legal para proteger los derechos sexuales de los jóvenes?
¿Qué hacemos?
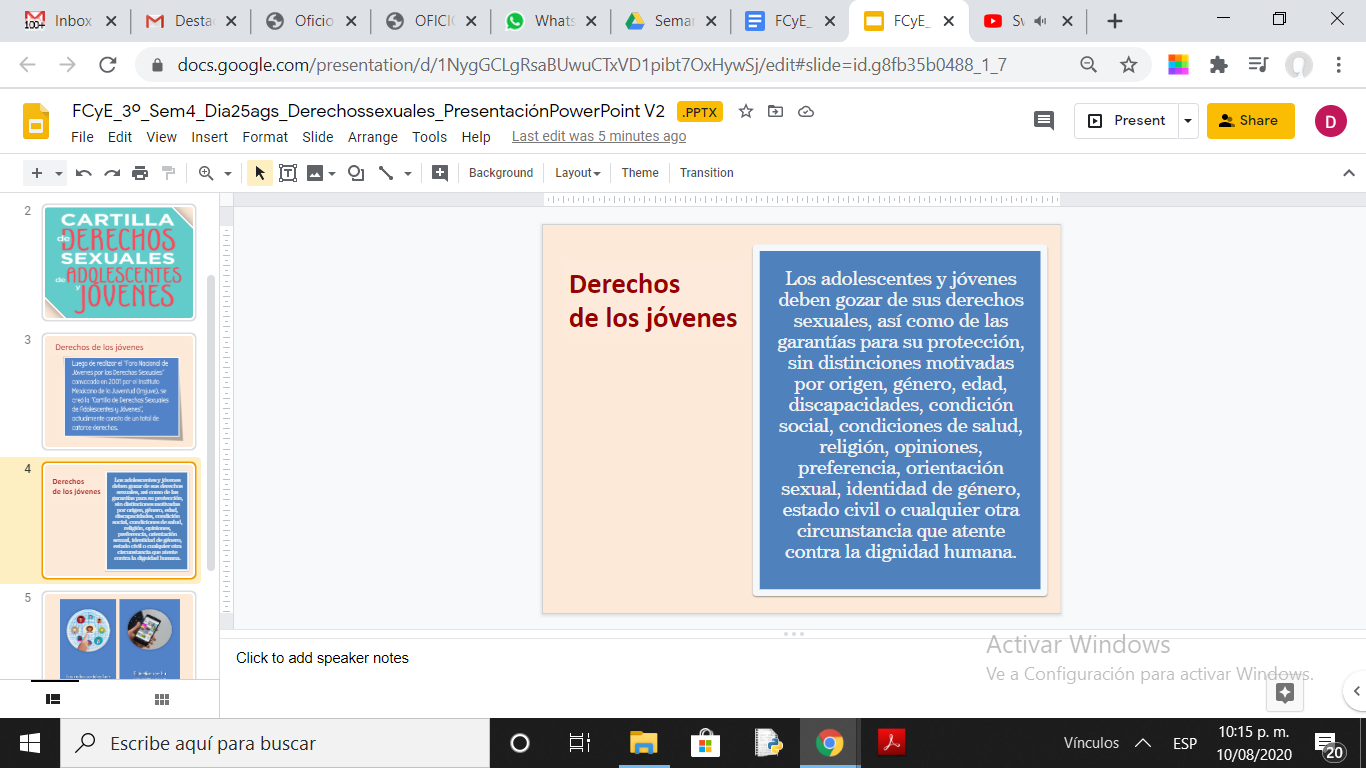
Para abordar propiamente la cartilla, tienes un primer grupo de derechos que hablan acerca de decidir libremente y con total autonomía sobre tu cuerpo, tus afectos, tu disfrute, y por supuesto, con quiénes te relacionas.
¿Qué condiciones o situaciones crees que son las que obstaculizan o impiden que los adolescentes decidan libremente y de forma autónoma e informada sobre su sexualidad?
Otro tema de gran relevancia en estos tiempos es que las redes sociales han generado nuevas formas de relacionarnos, es quizá el tema de la privacidad, la intimidad, y el derecho a vivir libres de violencia. ¿Cuáles son las situaciones o condiciones que los adolescentes deberían tener en cuenta para cuidarse a sí mismos y a las demás personas?
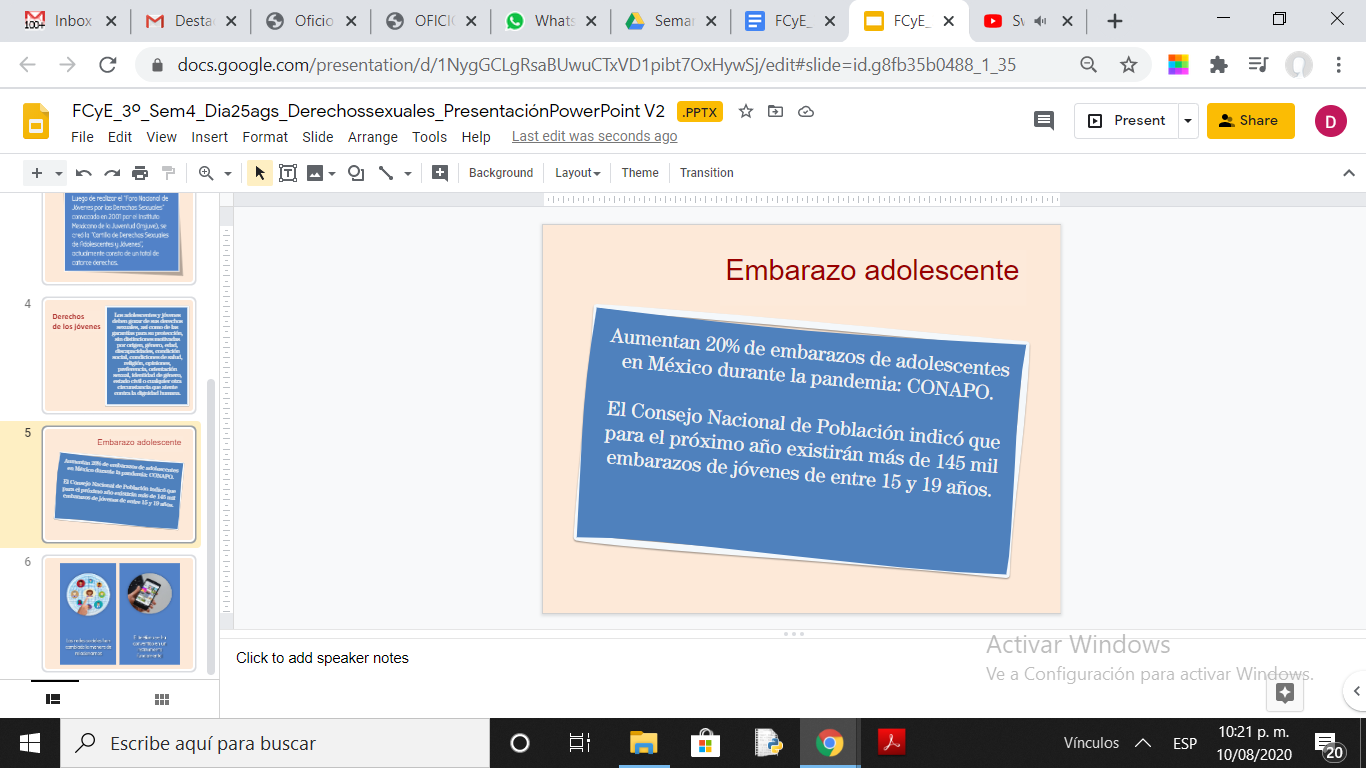
En estos tiempos de pandemia y de distanciamiento social, debes profundizar en el autocuidado en todas sus dimensiones. El Consejo Nacional de Población, ha alertado sobre el hecho de que durante la pandemia han aumentado 20% los embarazos en México.
Es por ello que no debes dejar de lado el derecho a decidir de manera libre e informada sobre tu vida reproductiva. ¿Cuáles crees que sean los dilemas o retos actuales más importantes para que los jóvenes decidan libremente sobre su vida reproductiva?
¿Cómo podrías ejercer plenamente tus derechos sexuales y reproductivos en este contexto tan complicado de distanciamiento social?
En el siguiente link puedes encontrar la Cartilla de Derechos Sexuales de Adolescentes y Jóvenes.
http://www.imss.gob.mx/sites/all/statics/salud/cartillajovenes2016.pdf
El reto de hoy:
Elabora un mapa mental con las ideas principales que escribiste en tu cuaderno.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:


Login to join the discussion