Las libertades individuales son de todos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:14Aprendizaje esperado: Analiza el papel del Estado y la ciudadanía en la vigencia y garantía del derecho a la libertad de las personas
Énfasis: Reconocer la función del Estado como garante de las libertades.
¿Qué vamos a aprender?
El propósito de esta sesión es reconocer la importancia y la función del Estado como garante de nuestras libertades.
Es necesario tener a la mano tu cuaderno de notas, hojas de colores, tijeras, pegamento y regla. Recuerda que puedes hacer uso del material con el que cuentes y tengas a tu alcance.
Si en este momento no cuentas con alguno de los recursos, puedes concluir tus actividades al término de la sesión.
¿Qué hacemos?
Como has visto a lo largo de tu formación, la libertad es un derecho humano que se ha defendido con la participación de muchas personas que se atrevieron a enfrentar y denunciar injusticias civiles por parte de particulares, gobiernos y gobernantes que abusaron de las personas más vulnerables, utilizando la violencia y la discriminación por parte de grupos sociales minoritarios que no consideraban el respeto y reconocimiento a la diversidad, la inclusión, la equidad y la igualdad de todos los seres humanos.
Por ello hoy en día, y en cada país, el Estado tiene la obligación de garantizar y proteger el ejercicio de las libertades de su ciudadanía; principalmente en un sistema democrático es fundamental cumplir y hacer cumplir el respeto y la protección a las libertades de todas las personas.
Para ello, es conveniente conocer el marco normativo y jurídico nacional e internacional, así como los propósitos de las instituciones que participan y tienen la facultad de regular las acciones para hacer respetar las libertades de la población.
Hablando de documentos internacionales, uno de los principales es la Declaración Universal de Derechos Humanos que, en sus dos primeros artículos proclama que todas las personas nacen libres e iguales en dignidad y derechos y que toda persona tiene todos los derechos y libertades proclamados en ella, sin distinción alguna de raza, color, sexo, idioma, religión, opinión política o de cualquier otra índole, origen nacional o social, posición económica o cualquier otra condición.
Por otro lado, en el preámbulo del Pacto Internacional de Derechos Económicos, Sociales y Culturales, se señala que “no puede realizarse el ideal del ser humano libre, liberado del temor y de la miseria, a menos que se creen condiciones que permitan a cada persona gozar de sus derechos económicos, sociales y culturales, tanto como de sus derechos civiles y políticos”.
Sin embargo, es importante señalar que cada Estado debe realizar acciones para establecer procesos jurídicos, supervisar la función de las instituciones al alcance de la población y garantizar el reconocimiento de las libertades que parten de los acuerdos internacionales firmados y ratificados.
Cabe señalar que dichos acuerdos tienen como propósito esencial, adoptar medidas, con apoyo y cooperación internacional para crear condiciones que favorezcan que cada persona disfrute de sus derechos civiles, culturales, económicos, políticos y sociales.
La posibilidad de vivir la libertad con dignidad tiene su fundamento en la Declaración Universal de Derechos Humanos, la Convención Americana sobre Derechos Humanos y otros tratados internacionales como:
- Pacto Internacional de Derechos Económicos, Sociales y Culturales (1966)
- Pacto Internacional de Derechos Civiles y Políticos (1966)
- Convención Internacional sobre la Eliminación de todas las Formas de Discriminación Racial (1965)
- Convención Internacional sobre la Eliminación de todas las Formas de Discriminación contra la Mujer (1979)
- Convención contra la Tortura y Otros Tratos o Penas Crueles, Inhumanos o Degradantes (1984)
- Convención sobre los derechos del Niño (1989)
- Convención internacional sobre la protección de los derechos de todos los trabajadores migratorios y de sus familiares (1990)
De acuerdo con lo señalado en el artículo 40 de la Constitución Política de los Estados Unidos Mexicanos, nuestro país es una República representativa democrática. Esto quiere decir que es el pueblo quien tiene el poder público a través de los Poderes de la Unión; asimismo, el respeto a las leyes es primordial y en ellas se deben garantizar las libertades y los derechos humanos.
En este sentido, como viste en grados anteriores, la Carta Magna establece las libertades y, al estar escritas en ese documento, se les llama fundamentales.
Recuerda algunas de ellas, para eso te sugerimos que tomes tus materiales para comenzar con la construcción de un organizador gráfico que irás complementando a lo largo de la sesión.
Observa y trázalo:
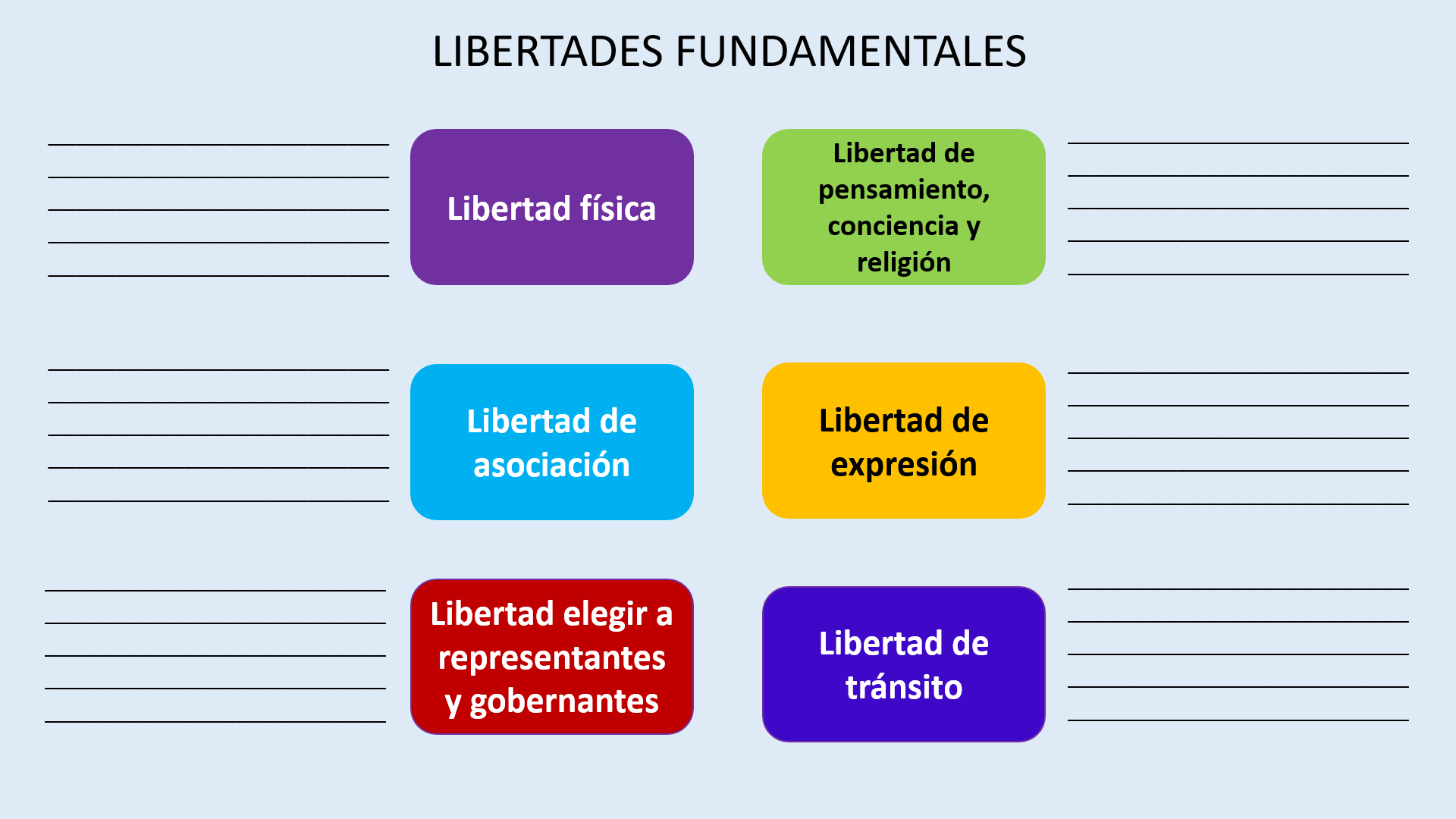
Como puedes observar, se señalan algunas libertades fundamentales:
Éstas son sólo algunas de las que están contenidas en la Constitución.
Como puedes observar, hay algunas líneas donde se te propone que especifiques el artículo constitucional y una paráfrasis o referencia de su contenido. Por ahora, revisa un ejemplo y te sugerimos que, al término de la sesión, complementes los faltantes.
En el caso de la libertad física, está establecida en el Artículo 1º y señala que “en los Estados Unidos Mexicanos todas las personas gozarán de los derechos humanos (…), así como de las garantías para su protección (…). [Asimismo] Está prohibida la esclavitud (…)”.
Realizar este análisis, no sólo implica que recuerdes las libertades fundamentales a las que tienes derecho, sino que se planteen la pregunta, ¿tener asentado en las leyes las libertades es lo único que puede hacer el Estado para garantizarlas?
No es suficiente, la Oficina del Alto Comisionado de las Naciones Unidas para los Derechos Humanos realizó la publicación “Prácticas de buen gobierno para la protección de los derechos humanos”, y en ese documento se menciona que para generar entornos propicios y favorecedores para la aplicación de los derechos humanos. Además de los marcos jurídicos que ya se mencionaron, debe haber instituciones y procesos políticos, administrativos y de gestión que los garanticen.
Esto quiere decir que debe existir un Estado de Derecho Democrático, que se refiere a un Estado donde se aplica un marco jurídico respetando las garantías fundamentales de las personas, quienes pueden hacen llegar a los gobiernos su sentir y expresan sus necesidades, así como participar en las acciones y en las decisiones. En síntesis, el Estado de Derecho representa la forma de vivir, considerando el poder de los Ciudadanos para decidir y participar, respetando la Ley.
Observa el siguiente video para comprender mejor la información.
- Los rasgos del Estado de Derecho democrático 19 seg.
En resumen, los derechos humanos representan los valores para vivir, reconocen la diversidad, se definen como un conjunto de facultades que garantizan la dignidad, colocándonos en igualdad de circunstancias ante la justicia, el estado y la sociedad; representan la esencia humana y permiten el desarrollo de las potencialidades, permiten actuar de manera libre y te protegen contra abusos de autoridades, particulares y servidores públicos.
El Estado de Derecho permite que los derechos humanos contribuyan al desarrollo integral de las personas; posee dos características principales:
- Las leyes permiten regular el comportamiento de los ciudadanos y sus representantes.
- El reconocimiento y protección de los derechos humanos que se representan en las libertades de los ciudadanos.
Los estados democráticos se identifican:
- porque expresan las diferencias de pensamiento.
- se reconocen los derechos de las personas.
- se expresa la pluralidad, es decir la diversidad en las formas de pensar.
- favorece realizar propuestas, de manera organizada, para dar solución a diversos aspectos como:
-
- Salud
- Educación
- Identidad
- Libertad de tránsito
- Residencia
- Manifestación de las ideas
Atienden la seguridad pública mediante acciones que permitan mantener el orden, hacer cumplir las leyes y fomentar los principios éticos de la sociedad, generando confianza en las personas.
México es un país que tiene un sistema de gobierno democrático, sin embargo, existen muchos retos que deben atender para consolidarse como un Estado de Derecho, debido a las problemáticas de orden social que afectan la legalidad, la impartición de justicia y el respeto a los derechos humanos; estas problemáticas que aquejan a nuestro país son:
- Corrupción
- Violencia (social y de género)
- Inseguridad
- Pobreza
- Salud
- Educación
- Desempleo
- Inequidad
- Deterioro ambiental
Es necesario atender, de manera urgente, estas condiciones que afectan el ejercicio de las libertades con una la base jurídica que garantice la seguridad de las poblaciones, mediante acuerdos con instituciones nacionales e internacionales, públicas y privadas, para atender y dar respuesta a actos de corrupción y omisiones ante los debidos procesos legales.
Para que puedas exigir la garantía de tus libertades, además de conocer las leyes, también debes conocer las instancias que están dedicadas, específicamente, a cada una de ellas. Es por eso que se te pide que retomes tu organizador gráfico y agregues, a cada una de las libertades, las instituciones que el Estado ha generado para garantizar las libertades o que contribuyen a ello.
Observa el ejemplo, para el caso de la libertad física, establecida en el artículo 1º constitucional, algunas de las instancias dedicadas a garantizarla son la Secretaría de Seguridad y Protección Ciudadana, la Secretaría de Relaciones Exteriores, la Comisión Nacional de los Derechos Humanos, Instituto Nacional de las Mujeres, el Consejo Nacional Para Prevenir la Discriminación, entre otros.
Te preguntarás si actualmente hay casos de esclavitud; desafortunadamente sí los hay, de hecho, se estableció el 2 de diciembre como el Día para la Abolición de la Esclavitud, al celebrarse el Convenio para la Represión de la Trata de Personas y de la Explotación de la Prostitución Ajena. Hay quienes piensan que esto es algo ajeno y que en nuestro país no hay situaciones de lo que se llama esclavitud moderna, pero es desafortunado que sí exista la trata de personas, el trabajo forzoso y el matrimonio infantil.
Una situación de este último es, por ejemplo, que en la alcaldía Milpa Alta, donde, según el Reporte Especial de Situación de las niñas y de las adolescentes en la Ciudad de México de 2018, “casi una de cada 200 niñas ya está casada o unida a la edad de 13 años”.
Es importante que reflexiones en las situaciones que obstaculizan cada una de las libertades, ya que, si bien el Estado es quien debe garantizar su cumplimiento, pero también debes buscar ambientes en donde se garanticen los derechos, ya que en algunos casos interviene la cultura.
En el documento “Prácticas de buen gobierno para la protección de los derechos humanos”, que ya se había mencionado, se analizan 21 casos en el mundo en donde se han llevado a cabo avances importantes para proteger los derechos humanos. Este estudio concluye que:
- La protección de los derechos humanos requiere marcos jurídicos nacionales compatibles con los principios de derechos humanos.
- La participación ciudadana y las distintas alianzas sociales son decisivas para la protección de los derechos humanos.
- La negociación y la creación de consenso favorecen la transformación de las prácticas sociales y legales para la protección de los derechos humanos.
- El acceso a la información y la transparencia contribuyen a la protección de los derechos humanos.
Adicionalmente, hay que agregar que, en el país, desde el marco legal y normativo, le compete al estado realizar las siguientes acciones:
- Compromisos del Estado Mexicano con la firma de convenios internacionales en materia de Derechos Humanos.
- Revisión, análisis y perfeccionamiento de las normas jurídicas, para evitar inconsistencias que afecten su ejecución.
- Establecer planes, programas y políticas públicas que contribuyan a respetar y hacer respetar el ejercicio y protección de las libertades como, por ejemplo, el Plan Nacional de Desarrollo 2019-2024.
- Contar con presupuestos que permitan llevar a cabo las acciones para su correcta ejecución.
- Diseño y construcción de espacios para la participación de la sociedad civil, difundiendo el derecho a la libertad.
- Crear acciones para evitar las prácticas de corrupción en las instituciones públicas y sancionar a quienes no cumplan con el respeto y la protección de las libertades.
- Mantener y preservar un Estado de Derecho democrático, aplicando la ley a quienes atenten contra los Derechos Humanos.
Al identificar tus libertades en la Constitución de los Estados Unidos Mexicanos, estas conscientes de que las instituciones que conforman el Servicio Público y la Administración Federal deben cumplir con la norma jurídica que regula y hace cumplir los lineamientos que protegen y garantizan las libertades de los ciudadanos, sin embargo, es obligación de los ciudadanos conocer y hacer valer estas leyes y, en su defecto, denunciar el incumplimiento de las mismas.
El gobierno tiene la función de regulador y protector del ejercicio de las libertades, sin embargo, la sociedad también tiene la responsabilidad de observar y participar, acudiendo a las instituciones que supervisan las violaciones a los derechos económicos, civiles y sociales en el país.
Recuerda también los principios de los derechos humanos; éstos son universales, en tanto son para todas las personas, sin distinción alguna, interdependientes e indivisibles, pues están desvinculados entre sí, pero tampoco pueden separarse unos de otros; finalmente, son progresivos, este principio es en el que, en esta sesión, hay que poner atención, pues es el Estado quien tiene el compromiso de, por un lado, no quitar lo que ya se ha ganado y, por otro, se deben adoptar las medidas necesarias para garantizar los derechos humanos a corto, mediano y largo plazo, conforme a las necesidades de la población.
Recapitula: Comenzaste por conocer los tratados internacionales que establecen los derechos humanos, mismos que ha firmado y ratificado nuestro país.
Realizaste un ejercicio que te permitió analizar cómo el Estado mexicano garantiza las libertades fundamentales, asimismo conociste las instancias que se han creado para protegerlas y garantizarlas, con la finalidad de reflexionar a dónde puedes acudir en caso de que las libertades sean violentadas.
Analizaste qué es un Estado de Derecho democrático y las problemáticas que impiden que se garanticen la libertad y los derechos de las personas.
También puntualizaste las acciones que tiene que llevar a cabo el Estado para que la población pueda ejercer sus derechos.
El Reto de Hoy:
Revisa tu libro de texto para ampliar la información de lo que has aprendido; también consulta los acuerdos internacionales que tiene nuestro país para proteger las libertades de toda la población. Estos los podrás encontrar, principalmente, en las plataformas de la Organización de las Naciones Unidas y de la Comisión Nacional de los Derechos Humanos.
Puedes participar más en la construcción de un sistema democrático incluyente, seguro y vigilante de la efectividad de los planes y programas que regulen las libertades en la vida cotidiana, sin obstáculos que los impidan; debemos informarnos para descubrir de qué manera puedes contribuir para alcanzar un Estado de derecho democrático que garantice y proteja el ejercicio de tus libertades.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:



Login to join the discussion