¿Cuál es la importancia de las reacciones redox en la industria?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:12
¿Cuál es la importancia de las reacciones redox en la industria?
Aprendizaje esperado: analiza los procesos de transferencia de electrones en algunas reacciones sencillas de óxido-reducción en la vida diaria y en la industria.
Énfasis: analizar los procesos de transferencia de electrones en algunas reacciones sencillas de óxido-reducción en la industria.
¿Qué vamos a aprender?
Se abordará en esta sesión la experimentación como una herramienta básica en el quehacer científico.
Lee la siguiente frase célebre del gran científico e inventor estadounidense Benjamín Franklin.
La oxidación, por falta de uso, gasta mucho más las herramientas que el propio trabajo.
Reflexiona en torno a la frase y escribe en tu cuaderno tu impresión acerca del significado.
Por medio de la experimentación podrás observar lo que sucede durante una reacción redox relacionada con la industria, lo cual te permitirá comprender las reacciones de una forma más sencilla.
También recuerda registrar en tu cuaderno la información que consideres importante, así como aquellos ejemplos que te ayuden a comprender el tema.

Se le conoce como “Gran Oxidación” al momento de la historia de la Tierra cuando hubo un crecimiento importante en la cantidad de minerales.
Este acontecimiento provocó la oxidación de minerales preexistentes, produciendo las primeras apariciones de hasta dos tercios de los minerales que existen hoy en día.
Esto ocurrió cuando el oxígeno comenzó a acumularse en la atmósfera de la Tierra, hace unos 2 200 millones de años.
Los materiales que utilizarás son tu libro de texto de Ciencias. Química, tu cuaderno, así como bolígrafos, colores y tijeras.
NOTA para los docentes:
Consulta el libro “Enseñando química: material de apoyo para profesores de secundaria”, que forma parte de la serie “Enseñando Ciencias”.
Es un texto dirigido a profesores de secundaria que imparten la asignatura de Química.
Este material está integrado por cinco grandes apartados escritos por experimentados profesores de Química de la UNAM en sus muy particulares áreas de especialización.
Cada uno de los apartados, descritos y abordados con rigor académico, contienen explicaciones amenas y sencillas, así como recomendaciones de aplicación en el aula.
Pueden descargarlo de forma gratuita en formato PDF visitando la siguiente dirección electrónica: http://villaeducacion.mx/?mod=categorias&idtema=5653
¿Qué hacemos?
La atmósfera del planeta Tierra es oxidante porque en ella hay 21% de oxígeno. Muchos minerales son óxidos, y en el suelo se encuentran silicatos u óxidos de silicio. Una de las moléculas más abundantes en la Tierra es el agua u “óxido de hidrógeno”.
Todos los metales y minerales son importantes para la vida diaria, ya que muchos productos indispensables provienen de ellos; sin embargo, el proceso de obtención de los metales no es tan sencillo, ya que muchos de ellos no se encuentran en forma pura en la naturaleza y son obtenidos por medio de procesos industriales conocidos como metalurgia.
Las reacciones de óxido-reducción se presentan con frecuencia en estos procesos.
La obtención del hierro es un ejemplo de obtención de un metal por reducción a nivel industrial.
La metalurgia del hierro recibe el nombre de siderurgia. Uno de los principales métodos utilizados para reducir el mineral de hierro, por lo general, hematita Fe2O3, en donde se suelen encontrar impurezas como los silicatos, es el denominado “alto horno”.
La reducción se lleva a cabo mediante el monóxido de carbono, que se genera a partir de la reacción del coque, que es una forma de carbono, con el oxígeno del aire, para producir dióxido de carbono y calor, a la misma vez que se le proporciona calor.

El alto horno es un reactor químico que funciona contra corriente. Los gases suben mientras que los sólidos se dirigen hacia abajo, lo que le proporciona un rendimiento térmico excelente, ya que el hierro se reduce en etapas que dependen de la temperatura.
La parte alta del horno es donde la temperatura es más baja, lo que facilita la formación de óxido de fierro Fe2O3, el cual, al descender a la parte más caliente, se reduce a FeO, que al final acaba por reducirse a hierro en la parte más caliente.
Has visto al hierro oxidarse en objetos como los clavos o las ventanas al tener contacto con la humedad y el aire del medio ambiente. El óxido de hierro es de color marrón y también se puede percibir en algunas piezas de automóvil y en las tuberías que se utilizan para la distribución del agua potable.
¿Conoces otros ejemplos de oxidación del hierro? Es muy importante observar con atención el entorno y estar al pendiente del cuidado de estos materiales.
En esta ocasión se va a llevar a cabo la reacción redox del hierro. Detecta los cambios que pueden ocurrir en este metal tan común.
¿Qué necesitas?
- Una disolución de sulfato de cobre, CuSO4
- Dos clavos grandes
- Cuatro clips
- Un vaso de precipitados de 250 ml
- Pinzas con punta
¿Cómo se hace?
•Agrega 150 ml de la disolución de sulfato de cobre, CuSO4, en el vaso de precipitados, teniendo cuidado de no salpicar.
•Coloca los clavos y los clips en la disolución y espera unos minutos en lo que se lleva a cabo la reacción química de estas sustancias.
Toma nota de las ecuaciones, para que en ellas puedas detectar qué elemento se oxida, y, por consiguiente, qué elemento se reduce.

Cuando el sulfato de cobre reacciona con el hierro, se forma cobre metálico, que se ha impregnado en el clavo, y un compuesto llamado sulfato de hierro que está en disolución. ¿Cuál se oxida? Asigna el número de oxidación de cada elemento.
En esencia, las reacciones redox implican la transferencia de electrones, esto es, el paso de electrones de un átomo que se oxida hacia uno que se reduce. Por lo tanto, si un elemento químico se oxida es porque pierde electrones y si el elemento se reduce, entonces se dice que ha ganado electrones.
En toda reacción química el número de cargas eléctricas positivas debe ser igual al de cargas negativas. Esto ya lo aprendiste en sesiones anteriores, así que sólo repasarás algunas reglas prácticas. Para saber cuándo un elemento pierde electrones o los gana, debes asignar el número de oxidación a cada elemento.
Al oxígeno en sus compuestos se le asigna un número de oxidación de menos dos, excepto en los peróxidos, en cuyo caso es menos uno.
Al hidrógeno en sus compuestos se le asigna un número de oxidación de más uno, pero cuando forma hidruros, se le asigna un valor de menos uno.
El número de oxidación de los elementos que se encuentran en estado basal o sin combinarse con otros es cero.
Para los elementos no especificados en las reglas se calcula por la suma algebraica de los números de oxidación, misma que deberá ser igual a cero, es decir, si existen cuatro cargas positivas, entonces también deberá de haber cuatro cargas negativas.
No olvides tener siempre a la mano tu tabla periódica, ya que es fundamental para la comprensión de este tema. Entonces asignarás el número de oxidación a cada elemento en la ecuación.
Antes recuerda que un elemento se oxida al perder electrones mientras que otro elemento se reduce ganando electrones.

En este caso, el ion sulfato tiene un número de oxidación de menos dos, por lo que se puede deducir que el del cobre es más dos y con esto se balancean las cargas eléctricas, que tienen el mismo número de cargas positivas que de negativas en el compuesto. El hierro, al encontrarse solo, tiene un número de oxidación de cero.
Al llevarse a cabo la reacción, se observa que el cobre se deposita en el clavo y queda separado del sulfato, éste reacciona con el hierro y se forma sulfato de hierro, por lo que ahora los números de oxidación se asignan de la siguiente manera.
El cobre, al estar solo, tiene un número de oxidación de valor cero. En el caso del sulfato, recuerda que es menos dos, por lo tanto, el hierro tendrá un número de oxidación de más dos, para tener el mismo número de cargas positivas que negativas en el compuesto.
Ahora observa las semirreacciones y determina cuál se oxida y cuál se reduce.

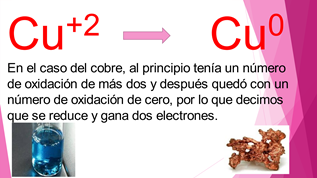
Los cambios que se dan en las reacciones redox pueden representarse en la recta numérica. Cuando un elemento cambia desplazándose hacia la derecha, se dice que dicho elemento se ha oxidado. En cambio, si pasa a una posición hacia la izquierda, entonces se dice que se ha reducido. En el ejemplo del hierro inicialmente su número de oxidación era de cero y pasó a más dos, entonces se dice que se oxida.
El cobre al principio tenía un número de oxidación de más dos y después quedó con un número de oxidación de cero, por lo tanto, se reduce.
Los procesos de oxidación y de reducción son complementarios, esto significa que un átomo no puede ganar electrones sin que otro los pierda. En toda reacción redox siempre hay un elemento que se oxida y otro que se reduce; además, el número total de electrones ganados de un átomo corresponde exactamente con la cantidad de electrones perdidos del otro.
Seguramente te has dado cuenta que muchos materiales que se usan están hechos de cobre, este material es usado en la fabricación de herramientas, tuberías, cables, alambre y en los componentes de una gran cantidad de aparatos electrónicos que se usan en la vida cotidiana, sin embargo, para obtenerlo es necesario recurrir a un proceso industrial.
Las herramientas hechas de cobre y sus aleaciones no producen chispas, por esta razón se utilizan en lugares en los que existen materiales volátiles como productos químicos o gases; de esta manera, se reduce el riesgo de explosión.
Aunque el cobre se obtiene de manera industrial a partir de un material llamado calcopirita, que es un mineral dorado y formado por sulfuros de cobre y hierro, se va a emplear una técnica muy antigua que era utilizada por gambusinos para obtener cobre metálico.
Ten presente que este tipo de actividades experimentales normalmente se llevan a cabo por un docente de la materia, ya que pudiera ocurrir algún accidente. Aprende cómo se efectúan las reacciones de óxido-reducción.
¿Qué se necesita?
●10 g de sulfato de cobre
●Una lámina o granalla de zinc
●Un vaso de precipitados
●100 ml de agua
●Una cuchara
¿Cómo se hace?
- Primero se disuelve el sulfato de cobre en agua.
- Se introduce la placa o granalla de zinc, con cuidado de no salpicar o tocar la disolución.
- Después de cinco minutos se saca el zinc y se observa lo que sucedió.
Se te recomienda sintonizar el programa aprende en casa II para que puedas observar los experimentos.
Cuando el zinc reacciona con el sulfato de cobre se forma sulfato de zinc y cobre metálico. ¿Qué reacción se está efectuando? Observa la siguiente ecuación.

Asignarás el número de oxidación a cada elemento en la ecuación para identificar si hay transferencia de electrones.

Recuerda que el ion sulfato tiene un número de oxidación de menos dos. En la fórmula del sulfato de cobre, el oxígeno tiene un número de oxidación de menos dos, por lo que, considerando el número de átomos de oxígeno, se tienen en total ocho cargas negativas.
Como el ion sulfato tiene un número de oxidación de menos dos, entonces el azufre tiene un número de oxidación de más seis, por lo que el cobre tendrá un número de oxidación de más dos para completar el mismo número de cargas positivas que de negativas en el compuesto, pues es eléctricamente neutro. Debido a que el zinc está en estado libre su número de oxidación es cero.
En los productos se observa que se formó el sulfato de zinc; siguiendo el mismo razonamiento que el sulfato de cobre, se dice que el ion sulfato tiene un número de oxidación de menos dos para balancear las cargas eléctricas y tener el mismo número de positivas como de negativas. Se deduce que el número de oxidación para el zinc es de más dos.
Por último, el cobre que está sin combinar tiene número de oxidación con valor de cero.
Ahora verifica qué elementos modificaron su número de oxidación. Se trata del zinc y del cobre.
¿Cuál elemento se oxida y cuál se reduce?
¿Cuántos electrones se transfirieron en cada caso?
¿Cuál elemento ganó electrones?
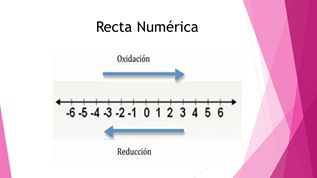
Recuerda que se puede emplear la recta numérica para ayudarte a identificar el elemento que se oxida y el que se reduce.
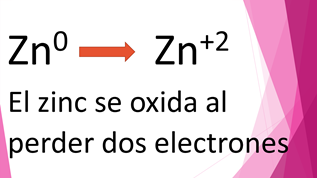
Analiza la semirreacción del zinc y observa que antes de reaccionar con otras sustancias, estaba como zinc cero, y después de la reacción se obtuvo zinc más dos; indicando que perdió dos electrones, por lo que se entiende que se oxidó.
Ahora bien, ¿qué le pasó al cobre? Observa la semirreacción.
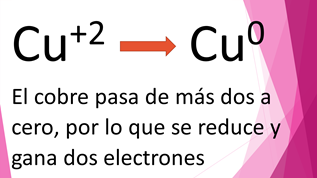
Inicialmente el cobre estaba como cobre más dos y después de la reacción del sulfato de cobre con el zinc, el cobre quedó solo, con número de oxidación cero. Entonces el cobre pasa de más dos a cero, por lo que ganó dos electrones, por lo tanto, se dice que se redujo.

Las reacciones oxido-reducción son importantes en la industria, por ejemplo, en el caso de las celdas solares, se puede convertir la energía solar en energía eléctrica gracias a este tipo de reacciones. También para la obtención de metales, pues en general éstos se encuentran en la naturaleza formando óxidos.


Para repasar y confirmar el aprendizaje de esta sesión realiza la siguiente actividad.
•Coloca el número de oxidación de cada elemento químico de las ecuaciones e identifica qué elemento se oxida y cuál se reduce.
•Es importante que escribas cuántos electrones pierde el elemento que se oxidó y cuántos electrones gana el elemento que se redujo.
El cobre tiene la curiosa propiedad de reflejar distintos tipos de color.
Cuando se encuentra en forma de película delgada, se puede apreciar en color verde y de color rojo en piezas de mayor grosor.
El cobre expuesto al aire y la humedad pierde su brillo, se empaña, se vuelve mate y se torna verde. Esta capa no se incrusta, sino que lo recubre y lo protege, pero esto ya no es cobre, sino óxido de cobre.
Este metal es resistente a la corrosión por lo que tiene muchas aplicaciones, entre ellas, la creación de artesanías.
Santa Clara del Cobre, en Michoacán, es un pueblo mágico reconocido a nivel internacional por la creación de piezas artesanales utilizando este bello metal.
El reto de hoy:
Con la finalidad de promover el conocimiento sobre el arte popular mexicano, conoce el documento “El cobre y el hierro en la artesanía mexicana”, este cuadernillo monográfico publicado por el Fondo Nacional para el Fomento de las Artesanías (Fonart) presenta diversos temas relacionados a la creación popular. Escritos por distinguidos especialistas donde se describen la producción y usos del cobre y el hierro desde la época prehispánica.
¡Buen trabajo!
Gracias por tu esfuerzo.



Login to join the discussion