Guillermo González Camarena y la televisión a color
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54
Guillermo González Camarena y la televisión a color
Aprendizaje esperado: describe la generación, diversidad y comportamiento de las ondas electromagnéticas como resultado de la interacción entre electricidad y magnetismo.
Énfasis: analizar y reflexionar sobre cómo se logró el desarrollo tecnológico para pasar de la televisión en blanco y negro a la televisión a color.
¿Qué vamos a aprender?
Analizarás y reflexionarás sobre cómo se logró el desarrollo tecnológico para pasar de la televisión en blanco y negro a la televisión a color. Así como quién lo hizo posible. Nos referimos al Ingeniero mexicano Guillermo González Camarena.
¿Qué hacemos?
Como viste en sesiones anteriores, las telecomunicaciones han sido un sector con gran auge y desarrollo, que nos permiten compartir información entre lugares muy alejados.
En particular durante el confinamiento por la pandemia, han sido de vital importancia para que la educación en México pueda continuar sin que tengamos que asistir a las aulas.
Reflexiona acerca de su evolución y funcionamiento.
El televisor, tele o TV, como se le suele llamar, es un aparato electrónico destinado a la recepción y reproducción de imágenes y sonidos a distancia. El televisor es básicamente la parte final de todo el proceso televisivo. Éste comienza con la captación de las imágenes y sonidos de origen, es decir, cuando se graban los programas, y culmina cuando los espectadores ven las emisiones.
La televisión recoge años de conocimientos y experimentación en distintas áreas.
Los antecedentes más inmediatos son el cine, el teléfono y la radio. Con estas tres tecnologías se podían reproducir imágenes y transmitir sonidos a distancia por separado. La televisión vino a conjugarlo todo en un solo evento. Por cierto, estas tecnologías funcionan gracias a fenómenos electromagnéticos.
La televisión no es la excepción, es un aparato que convierte señales eléctricas en imágenes y sonido.
Actualmente tenemos televisiones ultraplanas que apenas tienen unos cuantos centímetros de grosor, y que nos ofrecen imágenes coloridas en ultra alta definición. Pero no siempre fue así, antes los programas de televisión se veían solo en blanco y negro, como si se tratara de una foto antigua con movimiento. ¿Cómo fue que pasamos de la televisión en blanco y negro a la de color?
Las investigaciones y experimentaciones para desarrollar los televisores iniciaron al final del siglo XIX. El primer prototipo exitoso fue la televisión electromecánica desarrollada por John Logie Baird en 1925.
Lo que hacía esta televisión era dividir las imágenes en puntos, esto se hacía con ayuda de un dispositivo llamado disco de Nipkow. Era un círculo con pequeñas perforaciones que seguían una espiral, cada orificio dejaba pasar la luz de una zona específica de la foto.
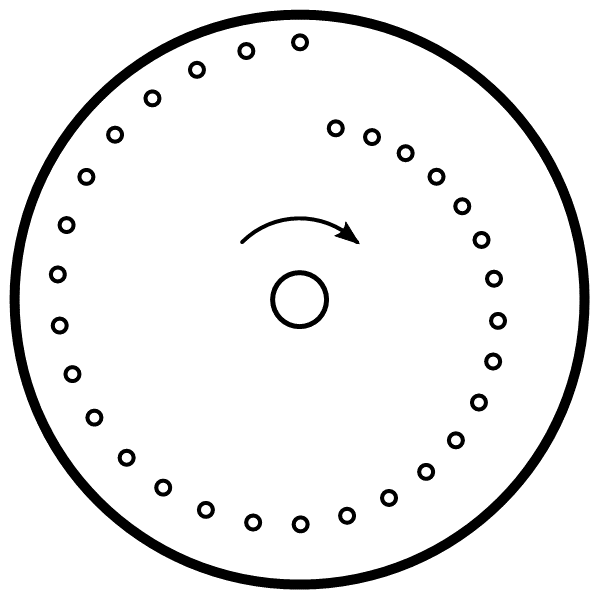
Y por la disposición de las perforaciones, se hacía un barrido de toda la imagen, dividida en puntos.
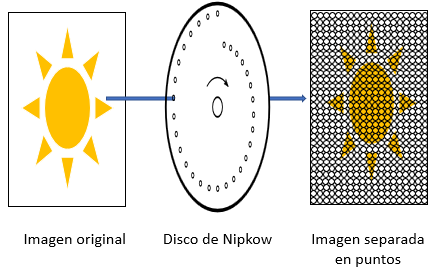
En las imágenes en blanco y negro, el único atributo que se capta es la luminosidad, es decir, qué tan claro u oscuro se ve algo. La intensidad de la luz de cada punto era convertida en un impulso eléctrico y luego llevado a través de un cable al emisor, que era una lámpara con otro disco de Nipkow.
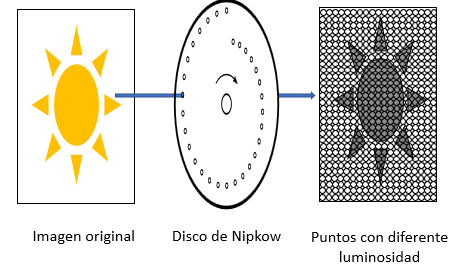
Con este arreglo se proyectaban puntos con distinta luminosidad. Lo que reproducía la imagen original.
Esta primera televisión solo servía para imágenes muy pequeñas, además estáticas y no transmitía sonidos.

Pero a partir de este logro, John Logie Baird puso la mira en la transmisión a grandes distancias. Para 1930 realizó la primera transmisión simultánea de audio y video.
Estos dispositivos se empezaron a comercializar y eran básicamente radios que podían proyectar imágenes. La era de la televisión moderna empezó en las primeras décadas del siglo XX, y muchas personas se dedicaban a su estudio.
Uno de estos investigadores era el inventor Philo Farnsworth, quien desde muy pequeño se interesó por los fenómenos electromagnéticos, de los que leía en libros y revistas.

Se dice que a la edad de 14 años había analizado la manera de formar imágenes utilizando electrones, así como cuando leemos un libro, en donde vamos recorriendo con los ojos letra por letra con un movimiento constante, avanzando de línea en línea. Esto se parece mucho a lo que hacían los discos de Nipkow, pero en lugar de utilizar luz, Philo quería usar electrones.
Después de 6 años, logró montar un pequeño laboratorio, donde experimentó con el uso de tubos de rayos catódicos.
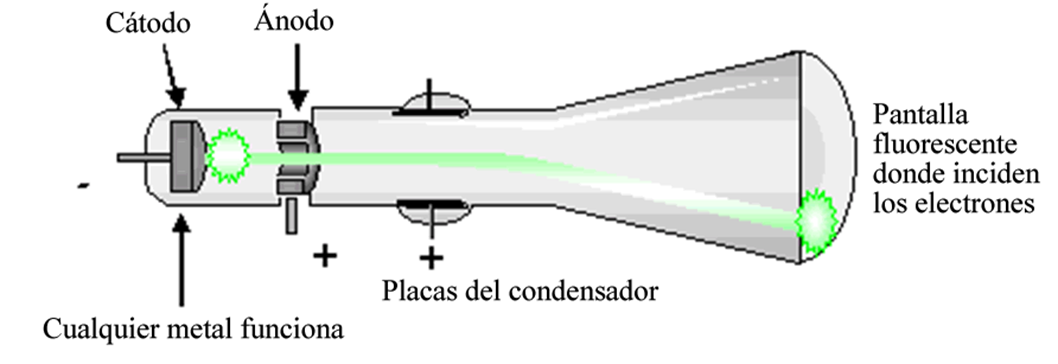
Estos están formados por un tubo de vidrio al vacío, dentro del cual se establece un flujo de electrones cuya trayectoria puede ser modificada por campos eléctricos y magnéticos, para que se estrellen con una pantalla de material fluorescente. Cuando impactan los electrones en dicha pantalla, se puede ver un destello.
En 1929, Philo había desarrollado un dispositivo que llamó disector de imagen. En éste, se transformaba la luz en impulsos eléctricos con ayuda de una pantalla fluorescente y un haz de electrones.

Al mismo tiempo, el ingeniero ruso nacionalizado estadounidense, Vladímir Zworykin, estaba trabajando en un instrumento similar, pero tenía algunos problemas que no podía resolver.

Visitó el laboratorio de Farnsworth, y con engaños lo convenció de que le hablara de su dispositivo, esta plática le ayudó a resolver las dificultades de su propia investigación.
Fue así como Zworykin concluyó la construcción de su propia cámara de televisión, la que recibió el nombre de iconoscopio.

Zworykin trabajaba para una gran compañía dedicada a la radiodifusión, y se enfrascaron en un pleito por la patente con Philo Farnsworth, quien los acusó de robo.
Dos años después, en 1931, el investigador y físico alemán Manfred von Ardenne,
hizo la primera demostración de un sistema de televisión que había desarrollado, donde usaba tubos de rayos catódicos para la transmisión y recepción de imágenes.

Esa tecnología fue mejorada y en 1936, fue utilizada para transmitir los juegos olímpicos de Berlín en toda Alemania.
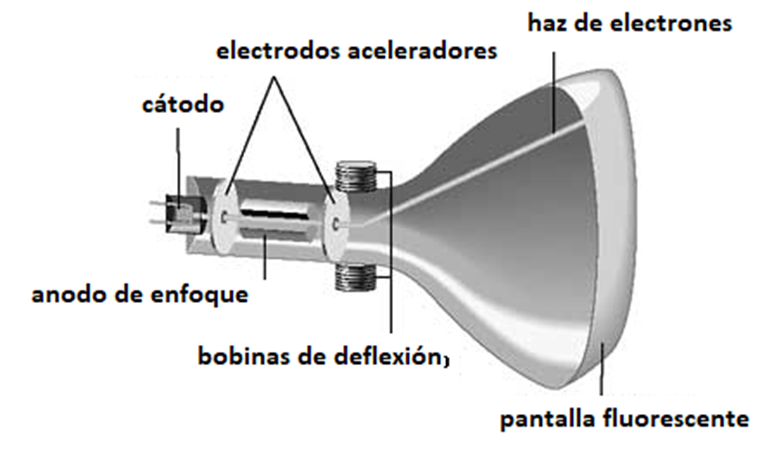
El tubo de rayos catódicos utilizado para la proyección de las imágenes en los televisores, recibe el nombre de cinescopio. En éste, el haz de electrones choca contra una pantalla recubierta con materiales fosforescentes, que se iluminaban con la energía de los electrones. La intensidad de la reacción producía zonas oscuras o claras produciendo una imagen en blanco y negro.
En el año de 1940, el ingeniero mexicano Guillermo González Camarena registra la patente en nuestro país, del primer sistema para televisiones a color del mundo.

Pero ¿Cómo fue el desarrollo de esta tecnología?, ¿y cómo es que funciona?
Para resolver esas preguntas, conocerás un poco de la vida del ingeniero Guillermo González Camarena.
Nació el 17 de febrero de 1917 en Guadalajara, Jalisco, siendo el más joven de siete hermanos. A la edad de dos años, su familia decidió mudarse a la ciudad de México.

Era un niño con una gran curiosidad científica, y muchos deseos de aprender. Vivir en la ciudad le brindó la oportunidad de estar enterado de los últimos descubrimientos a nivel mundial.
Una vez sabiendo leer y con conocimientos básicos en las matemáticas, a muy temprana edad, consultaba libros especializados para entender el funcionamiento del radio, y aunque le resultaban confusos debido a que solo era un niño y estaba recibiendo educación básica, sus esfuerzos no menguaban.
A los 7 años construyó una pequeña planta eléctrica con la que alimentaba algunos focos para ayudar a sus hermanos a que pudieran terminar sus tareas por la tarde. A los 8, fabricaba sus propios juguetes movidos por electricidad, con el paso de los años, su imaginación y habilidad crecían al igual que sus invenciones. Fue así que, siendo solo un adolescente de 12 años, construiría su primer transmisor de radio, incluso construyó su propio telescopio.
A los 13 se inscribe en la Escuela superior de ingeniería mecánica y eléctrica del Instituto Politécnico Nacional, donde coincide con los profesores Francisco Javier Stavoli y Miguel Fonseca, quienes realizaban experimentos con una televisión electromecánica. Es en este momento donde surge el interés del joven Guillermo en esta tecnología.
En 1932, a la edad de 15 años, consigue un trabajo vespertino como ayudante de operador de audio en la estación de radio XEDP, de la Secretaría de Educación, y posteriormente consigue su licencia como operador de radio. Dos años después, en 1934, con todo el dinero que había logrado ahorrar, más algunas aportaciones de su familia, logra comprar un kit de televisión que comercializaba la RCA en Estados Unidos, para promover el desarrollo de este medio de telecomunicación. El paquete incluía un iconoscopio de Zvorykin con un instructivo para conectarlo.
Guillermo tenía la idea de construir su propio sistema de recepción y proyección de imágenes, es decir, una cámara y una televisión.
En esta época era común ver caminar al joven González Camarena por los mercados de Tepito y la Lagunilla en la Ciudad de México, buscando piezas para terminar su sistema. En lo que algunas personas veían basura, el encontraba piezas útiles para sus inventos.
Como no había televisores en México en ese momento, Guillermo tuvo que usar un osciloscopio como monitor.

Los osciloscopios son instrumentos que nos permiten ver señales eléctricas, y en ese tiempo, tenían un tubo de rayos catódicos como pantalla.
Con el iconoscopio y las partes que había recolectado, logró construir una cámara de televisión, y en 1939, finalmente pudo obtener una imagen en su monitor. Además, en este mismo año, logró graduarse de la escuela de ingeniería.
Hasta este punto, González Camarena estaba replicando lo que acontecía en otros lugares del mundo, solo que su imagen no fue en blanco y negro, si no en color verde, debido a que la pantalla del osciloscopio estaba recubierta con un tipo de fósforo que, al ser impactado con electrones, emitía luz en ese color.
Es muy probable que esta variación en el color de la imagen fuera lo que lo impulsara a dedicar sus esfuerzos a la construcción de un sistema que produjera imágenes a color. Estas ideas siguieron haciendo eco en su mente, y solicitó la patente de lo que él denominó como “sistema tricromático de secuencia de campos” Aunque en este momento solo tenía la idea, y nada construido.
La idea original que tenía el ingeniero González Camarena consistía en adaptar una serie de filtros de colores a las cámaras y televisiones que ya existían, y que eran en blanco y negro. Cada filtro dejaría pasar solo una luz de color primario, es decir, azul, rojo o verde.

Entonces, cuando la luz pasa a través de esos filtros, solo dejará pasar la luz azul, roja o verde que provenga de lo que se esté grabando con la cámara de televisión.
Entonces, los sensores de las cámaras estarían detectando la intensidad de la luz en esos colores.
Digamos que es como si capturaran 3 imágenes, cada una formada solo por la luz de cada uno de los colores primarios.

De este modo, una cámara en blanco y negro podría recolectar información en tres colores ayudada por los filtros. Mientras que, en las televisiones, también en blanco y negro, se debían montar filtros, en este caso sobre la pantalla, para colorear las imágenes proyectadas. Los filtros de la pantalla debían moverse en sincronía con los de la cámara y con la velocidad suficiente como para que nuestro ojo no notara el cambio, e interpretara como si todos los colores se vieran al mismo tiempo.
Suena complicado, pero una vez que Guillermo González reveló sus ideas al tramitar la patente, varios investigadores en Estados Unidos empezaron a trabajar utilizando ese mismo principio, por lo que el joven ingeniero tuvo que patentarla también en ese país, y así proteger sus ideas.

En 1946 se establece la primera estación experimental de televisión en México, con equipo diseñado y construido por el ingeniero González Camarena, que se identificaba con las siglas XEHGC y utilizaba el canal 5.
En 1948 fundó una empresa llamada Laboratorios GonCam, donde se fabricaban equipos de video, televisiones y telecomunicaciones. Fue ahí donde se estableció un circuito cerrado con el que se hicieron las primeras pruebas del funcionamiento de la televisión a color.

También se realizaban un sinfín de actividades privadas, gubernamentales y académicas. Para Guillermo González Camarena, era muy importante contribuir a la mejora de la educación de los jóvenes, es por eso, que en el año 1949 se implementaron equipos de televisión a color en un circuito cerrado para hacer la transmisión de una cirugía, dentro de la novena asamblea de médicos cirujanos, llevada a cabo en el Hospital Juárez.
Era tanto su interés en la educación, que una de las aplicaciones que más le interesaba para sus inventos, era la alfabetización, y en conjunto con la secretaría de educación pública, se sentaron las pautas para lo que se conocería como el sistema de educación de telesecundaria.
Realizó varios viajes a Chicago para conseguir los componentes para sus inventos, entablando comunicación con el Columbia College en dicha ciudad. En esta universidad se capacitaban técnicos en televisión, por lo que encargaron al ingeniero un sistema de circuito cerrado con dos cámaras, entregado en 1950.
Por esto le fue conferido el título de catedrático honoris causa en aquella institución.
También en 1950 comenzaron las trasmisiones de televisión comercial en la ciudad de México.
Al siguiente año contrajo matrimonio con María Antonieta Becerra Acosta, con quien más adelante procrearía dos hijos, Guillermo y Arturo.

En 1952 se concedió la frecuencia del canal 5, que se identifica como XHGC.

Fue hasta 1960 que se comenzaron a hacer las pruebas para grabar y transmitir la televisión comercial en formato de color, mismas que comenzaron a partir del 21 de enero de 1963, con la transmisión de la serie llamada “Paraíso infantil” por el canal 5.
En 1962 terminó el desarrollo de otro sistema de televisión a color, llamado “Sistema bicolor simplificado”. Éste funcionaba de forma muy similar al tricolor, pero solo se utilizaban dos filtros, tanto en la cámara como en el aparato receptor. El primer filtro captaba la contribución en colores rojos y naranjas, mientras que el segundo filtro hacía lo mismo, pero en los colores verdes y azules. Esta mejora hacía más eficiente todo el proceso, además de que reducía sus costos y hacía que los televisores fueran más accesibles.
Fue tanto el interés que despertó este invento en los fabricantes nacionales de televisiones, que el ingeniero González Camarena ideó y patentó un tipo diferente de cinescopio, recubierto de puntos con diferentes variaciones de fósforo, que podían emitir luz roja y azul, cuando eran impactados por un haz de electrones. Por lo tanto, el televisor ya no necesitaba los filtros, puesto que la pantalla ya era capaz de emitir luces de colores y no solo variaciones de luminosidad.
Es de este modo cómo funcionan las televisiones a color que cuentan con un cinescopio, en donde, la señal que puede provenir de estaciones transmisoras, o de aparatos de video, es traducida a un haz de electrones que aumenta o disminuye su intensidad gracias a un mecanismo de control. Esto se observa como un aumento o disminución del brillo de la pantalla cuando los rayos chocan contra ella.
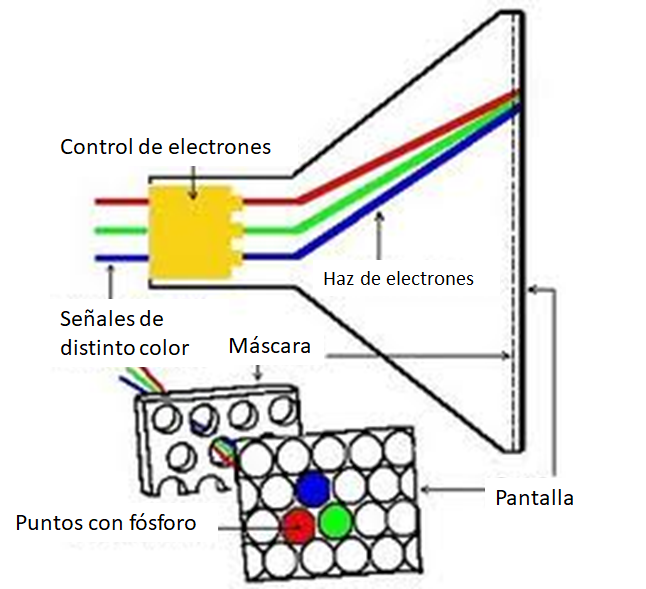
Las bases del tubo cuentan con dos bobinas deflectoras, estas bobinas generan campos magnéticos que varían a gran velocidad. La primera desvía el haz de electrones de izquierda a derecha y de derecha a izquierda, y la segunda, de arriba hacia abajo y viceversa.
La pantalla tiene en el interior de su cara frontal un revestimiento de fósforo con pequeños espacios de color azul, rojo y verde, mismos que brillan cuando son impactados por los rayos de electrones.

Guillermo González Camarena murió el 18 de abril de 1965, a la edad de 48 años, en un accidente automovilístico, y en señal de luto, se interrumpieron todas las transmisiones de televisión ese día.
Sin embargo, cuatro años después, derivado de la gran calidad de sus sistemas a color, la NASA los usó para transmitir las primeras imágenes desde la luna, en el programa apolo 11, y 7 años después en las ondas viajero 1 y viajero 2 para recibir imágenes del planeta júpiter, y de otros cuerpos celestes del sistema solar.

Si bien, las pantallas de televisión que se comercializan actualmente no utilizan más las tecnologías desarrolladas por Guillermo González Camarena, sus contribuciones han sido fundamentales para su desarrollo. Sin duda el Ingeniero Guillermo González Camarena fue un gran inventor.
Quienes lo llegaron a conocer comentan que no solo fue un gran inventor, también lo conocieron como un compositor, dibujante, astrónomo, zoólogo aficionado y estudioso de la historia y costumbres mexicanas.
Su muerte prematura interrumpió una gran cantidad de proyectos, por ejemplo, en 1954 solicitó una patente para un sistema de adaptación para la tercera dimensión en aparatos de televisión. Solo podemos imaginar hasta dónde hubiera llegado con su ingenio y pericia.
Guillermo González Camarena fue una pieza fundamental para el mundo moderno, sus inventos cambiaron la forma en la que nos comunicamos y entretenemos.
Recuerda que, si quieres resolver tus dudas o investigar más sobre el tema, puedes recurrir a páginas de internet confiables o libros especializados.
El reto de hoy:
Para concluir, te invitamos a que reflexiones acerca de las contribuciones de este personaje. Pregunta a tus familiares si alguno tuvo una televisión en blanco y negro, y pide que te cuenten cuáles eran sus características y cómo se veían las imágenes.
Si en tu hogar tienes una televisión con cinescopio, intenta acercar un imán y observa lo que pasa con la imagen. Pero ten cuidado de no dejar el imán en la misma posición mucho tiempo, pues la sustancia que recubre la pantalla se puede quemar debido al gran flujo de electrones, y dejar una mancha permanente.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas


Login to join the discussion