Bioconstruyendo la célula procarionte y eucarionte
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54Bioconstruyendo la célula procarionte y eucarionte
Aprendizaje esperado: identifica las funciones de la célula y sus estructuras básicas (pared celular, membrana, citoplasma y núcleo).
Énfasis: distinguir entre células procariotas y células eucariotas.
¿Qué vamos a aprender?
En esta sesión revisarás un divertido juego que te permitirá conocer más sobre los tipos de células. De esta manera se continuará con el desarrollo del aprendizaje esperado: Identifica las funciones de la célula y sus estructuras básicas (pared celular, membrana, citoplasma y núcleo). Teniendo como propósito: Distinguir entre células procariotas y células eucariotas.
¿Qué hacemos?
Hay dos tipos de juego, uno es Bioconstruyendo la célula eucarionte y el otro se llama Bioconstruyendo la célula procarionte.
Si recuerdas en sesiones anteriores, se explicó que en la naturaleza existe una gran diversidad de formas de vida que va desde las microscópicas unicelulares hasta organismos muy grandes, pluricelulares.
Fue Robert Whittaker quien propuso la clasificación en cinco reinos, la cual se basaba en el tipo de célula, el número de células y el tipo de nutrición.
En la sesión anterior se mostró que, aunque los organismos son muy diferentes, a nivel celular, se comparten varias características. Para comprenderlo se puede retomar la teoría de Darwin que menciona que todos los seres descienden de un ancestro común.
Asimismo, Lynn Margulis en colaboración con Karlene V. Schwartz mantuvieron, con algunas modificaciones, el sistema de cinco reinos. Y, tomando en cuenta la evolución biológica, los biólogos han construido varios árboles filogenéticos. Derivado de lo anterior, se puede mencionar que todos los organismos de los cinco reinos tienen un “ancestro universal común”.
Los biólogos señalan que el ancestro común, denominado LUCA, por sus siglas en inglés, lo cual traducido al español significa "Último Ancestro Común Universal”, fue un organismo unicelular del que probablemente evolucionaron, durante miles de millones de años, todos los seres vivos que existen actualmente, formados por células procariotas y eucariotas.
¡Así es! Fue con el descubrimiento y uso constante del microscopio que los biólogos reconocieron la existencia de dos tipos de células: procariotas y eucariotas. La característica que se tomó en cuenta para denominarlos es la presencia o ausencia de núcleo. De ahí surge el nombre procariota, es decir, antes del núcleo, representado por el reino Monera. Y eucariota, que significa núcleo verdadero. Constituyen a los reinos Protista o Protoctista, Fungi, Plantae y Animalia.
Interesante el origen de estos conceptos y su clasificación. Tomando en cuenta esta información: ¿qué te parece si revisas una ejemplificación del juego Bioconstruyendo la célula procarionte”?
Imagina que hay dos personas que llevarán a cabo este juego una es Rodolfo y la otra persona es Jaqueline:
Rodolfo:
Vamos a sacar el juego de su caja.
Jaqueline:
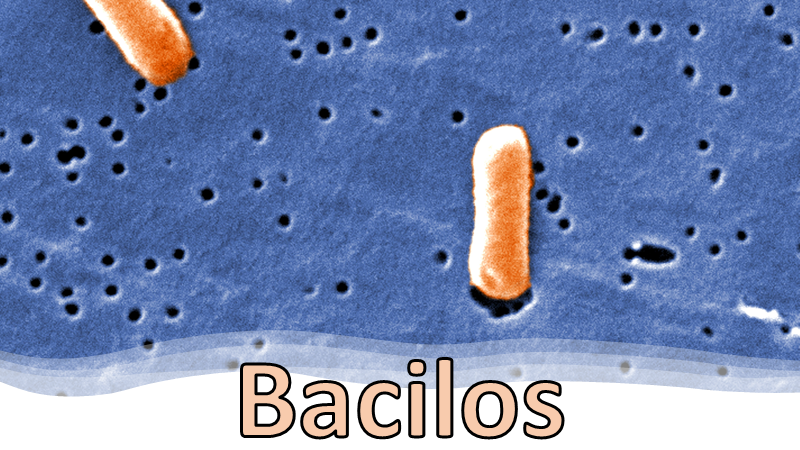
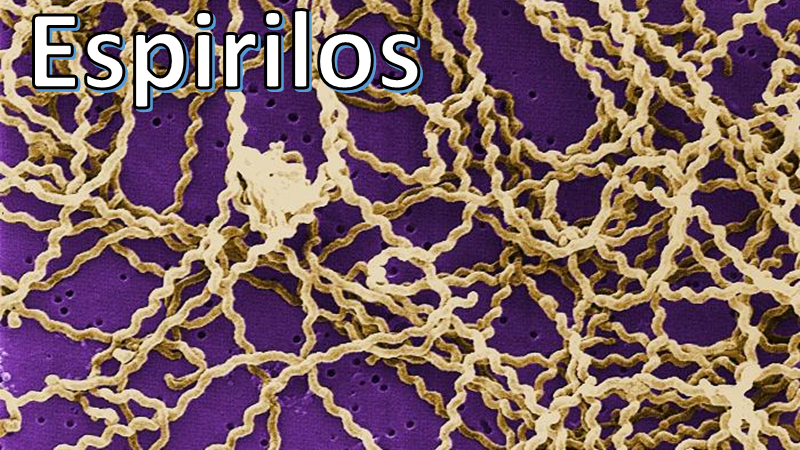
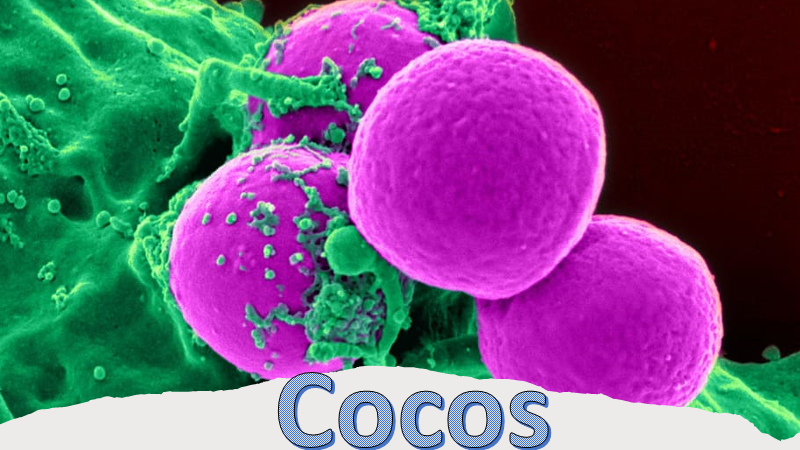
La tapa dice: “se calcula que las células procariotas existen desde hace más de 3,500 millones de años y fueron las únicas habitantes por más de 2,000 millones de años; actualmente, son los organismos más abundantes en la Tierra. Es en el reino Monera donde se encuentra una diversidad de formas de bacterias, como: bacilos, espirilos y cocos”.
 |
 |
 |
Rodolfo:
¡Muy buen dato! Vamos a pegar tu tablero en una pared, para que se pueda observar la membrana de la célula; que tiene la función de aislar el contenido celular del entorno y regular la entrada y salida de materiales de la célula.
Jaqueline:
El juego también incluye las imágenes de las diferentes estructuras, las cuales se van a ir pegando cuando se logre sacarlas del Bioconstruyendo.
Rodolfo:
¡Listo! ¿Gustas empezar, Jaqueline?
Jaqueline:
¡Gracias!, pero he de advertir que mi pulso no es nada estable.
(Toma unas pinzas y se prepara para sacar la primera pieza).
Rodolfo:
Entonces deberás tener mucho cuidado, pues recuerda que debes ir sacando las partes de la célula sin tocar los bordes. En caso de que los toques se escuchará un sonido. Y perderás tu turno.
Jaqueline:
Bueno, lo haré lentamente.
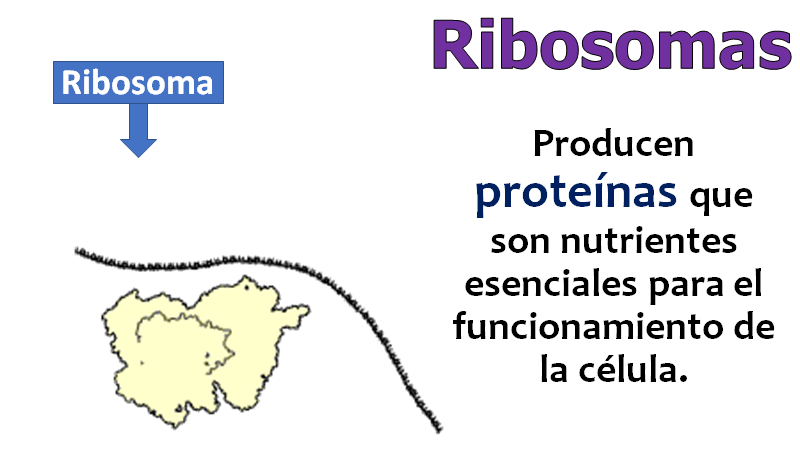
(Se acerca al juego y saca al ribosoma).
¡Qué bien! Pude obtener los ribosomas.
Rodolfo:
¡Lo hiciste muy bien!
(Toma una tarjeta del ribosoma y lee la información).
Jaqueline:
Pega la imagen en el tablero.
Rodolfo:
En la tarjeta de información se menciona que en esta estructura se producen proteínas que son nutrientes esenciales para el funcionamiento de la célula. Se encuentran flotando en el citoplasma, aunque en las células procariontes son más pequeños que en las eucariontes.
Jaqueline:
¡Interesante!, y hay muchos dispersos en todo el citoplasma.
Ahora es su turno, Rodolfo.
Rodolfo:
(Toma las pinzas y saca la pieza del ADN).
¡Sí! He obtenido el ADN o ácido desoxirribonucleico, que es el material genético.
Jaqueline:
(Toma la tarjeta y lee la información, mientras Rodolfo pega la imagen en el tablero).
En esta tarjeta se menciona que el ADN contiene toda la información para elaborar proteínas que controlarán las funciones del organismo procarionte. Tienen un cromosoma circular único que consta de dos largas cadenas enrolladas de ADN, el cual no cuenta con una membrana que lo recubra.
Rodolfo:
Así es, cabe mencionar que la reproducción de la célula procariota es asexual, usualmente por fisión binaria. La célula primero duplica su material genético, después aumenta su tamaño y finalmente se divide en dos.
Jaqueline:
¡Es mi turno!
(Toma las pinzas e intenta obtener la pared celular, pero suena el timbre que marca error).
¡Noooo, perdí!
Rodolfo:
Ni hablar, al parecer sí te falló el pulso. Ahora me toca a mí.
(Toma las pinzas y saca la pared celular).
¡Sí! Obtuve la pared celular.
Jaqueline:
(Toma la tarjeta y lee la información, mientras Rodolfo pega la imagen en el tablero).
Esta estructura protege y da soporte a la célula.
Rodolfo:
Claro y, como una de las partes básicas, permite que los organismos procariotas habiten ambientes extremos: con poca agua, con temperaturas muy elevadas, muy ácidos, entre otros.
Jaqueline:
(Observa el juego bioconstruyendo).
No puede ser, ya sólo quedan dos estructuras, espero que pierdas en tu siguiente turno Rodolfo, de lo contrario creo que me vas a ganar.
(Toma las pinzas e intenta obtener el flagelo).
Sólo espero no volver a equivocarme.
(Suena el timbre de error).
¡Nooo! Otra vez perdí mi oportunidad.
Rodolfo:
Ay, Jaqueline, no te preocupes. A veces se pierde y a veces se gana.
(Toma las pinzas e intenta obtener la pared celular y suena el timbre de error).
¡No puede ser! También toqué los bordes.
Jaqueline:
¡Siiií! Aún tengo oportunidad de ganar.
(Toma las pinzas saca el flagelo).
¡Qué bien!, pude sacar el flagelo.
Rodolfo:
(Toma la tarjeta y lee la información, mientras Jaqueline pega el flagelo).
De acuerdo con la información de la tarjeta, éste permite que la célula se mueva en un medio acuoso.
Ahora es mi turno.
(Toma las pinzas saca el plásmido).
¡Qué bien!, pude sacar el plásmido.
Jaqueline:
La tarjeta dice: son elementos extracromosómicos del ADN bacteriano. Están formados por una doble cadena de ADN, sólo que no siempre son circulares, hay especies en los que éstos son lineales.
Rodolfo:
Los plásmidos pueden contener información sobre la fertilidad, resistencia a un tipo de medicamentos o sustancias dañinas para las células. Esto permite explicar la resistencia de las bacterias a algunos medicamentos.
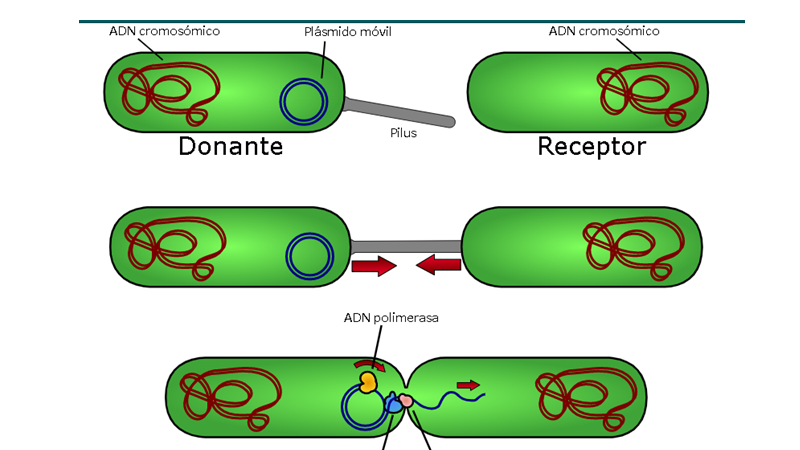
Mira Jaqueline, se completó el tablero, así que por nuestro gran trabajo en equipo lo declaramos como un empate.
Jaqueline:
¡Tienes razón! Creo que es lo justo.
Qué interesante ver sus estructuras, con las cuales puede realizar todas las funciones de los seres vivos, como nutrirse, respirar, relacionarse con el entorno y reproducirse.
Rodolfo:
Así es, ahora para identificar en qué se parecen y en qué son diferentes las células procariontes y eucariontes, vamos a ver mi juego de “Bioconstruyendo la célula eucarionte”.
Jaqueline:
¡Me parece perfecto, Rodolfo! Te ayudo a pegar tu tablero.
Rodolfo:
En mi caja también viene un dato.
Considerando la teoría endosimbiótica de la bióloga Lynn Margulis, las células eucariotas se originaron, probablemente, a partir de las células procariotas, por lo que se consideran las antecesoras de los organismos pluricelulares. Esta teoría está basada en el hecho de que las mitocondrias y los cloroplastos tienen su propio ADN, membranas y ribosomas para poder producir sus propias proteínas y reproducirse.
Jaqueline:
¡Woow! entonces eso quiere decir que, probablemente, una célula procarionte ¡fue absorbida por otra célula más grande! Ahora entiendo por qué es mayor el tamaño de tu tablero.
Rodolfo:
¡Así es! De acuerdo con los datos con los que cuentan los científicos, proponen que fue un evento casual de una mala digestión, es decir, que ciertos organismos procariotas absorbieron a otros procariotas más pequeños, pero no fueron capaces de digerirlas.
Así, probablemente, quedaron atrapadas dentro de la célula precursora de las eucariotas. Con el tiempo se hicieron simbióticas, es decir, ¡una dependía de la otra para sobrevivir!

Jaqueline:
Seguramente estás ¡impactado con esta información! Ya que, de esa forma, probablemente surgieron los organelos celulares de la célula eucarionte.
Rodolfo:
Esta interacción produjo el surgimiento de los primeros seres unicelulares eucariontes y continúa hasta estos días debido a la capacidad hereditaria de esta asociación endosimbiótica.
Jaqueline:
Muy interesante, ¡ya quiero ver las partes de tu célula!
Rodolfo:
¡Perfecto! Vamos a sacar las piezas para identificar qué estructuras contienen. Mira, aquí está la membrana celular.
(Señala el tablero).
Jaqueline:
Al igual que en la célula procarionte, es la que permitirá delimitar a la célula eucarionte, y como ya lo mencionamos, va acompañada del citoplasma, líquido importantísimo, que en este caso contendrá los organelos celulares.
Rodolfo:
¡Así es! Y precisamente aquí se tienen algunos organelos, como el núcleo, la mitocondria y el cloroplasto.
Jaqueline:
De manera muy general se puede decir que el núcleo contiene el ADN, rodeado por una membrana, toda la información genética se encuentra ahí. Pero, además, coordina la división celular, que puede dar origen a dos o cuatro células hijas, dependiendo del tipo de célula y el proceso que realice: mitosis o meiosis.
Rodolfo:
Por otro lado, la mitocondria también es un organelo ¡muy importante! ¿Te acuerdas del ATP, la moneda energética de los seres vivos? Pues bien, es la encargada de organizar esa transformación de la energía es la mitocondria.
Jaqueline:
El último organelo del Bioconstruyendo es el cloroplasto, estructura que se encuentra en células eucariotas de organismos productores que realizan fotosíntesis, es decir, el proceso por el cual logran transformar la energía luminosa en energía química.
Rodolfo:
Este proceso es muy importante, ya que es la base para el desarrollo de las cadenas y redes tróficas.
Jaqueline:
Se nos olvidan los ribosomas. Estos se encuentran en todas las células, y dentro de organelos, como las mitocondrias, cloroplastos y adheridos al Retículo Endoplásmico Rugoso. Estos pequeños paquetes son muy importantes para la síntesis de proteínas.
¡Ahora sí se tiene ambos tableros completos!
Rodolfo:
¡Woww! Son tan diferentes, pero también tienen similitudes.
Bien, después de haber revisado la ejemplificación anterior. Qué te parece si revisas el modelo de célula del proyecto de Ciencia escolar para identificar semejanzas y diferencias entre estos tipos de células.
Continuando con la elaboración, y enfocándose en algunos elementos que permiten diferenciar a las células procariontes de las células eucariontes.
¿Cuáles te imaginas que pueden ser?
La forma en cómo se presenta el material genético (ADN). En el caso de las células eucariontes, este elemento está almacenado en el núcleo, rodeado por una membrana. Pero en las procariontes, como se mencionó, se encuentra disperso en el citoplasma en forma circular sin contar con una membrana nuclear que lo delimite.
Para representar el material genético se utilizarán limpiapipas de dos diferentes colores. Al entrelazarlos te quedará una figura que integrarás a tu modelo. También puedes representar los plásmidos, formados por una doble cadena de ADN, más pequeña, que puede ser circular o lineal. Asimismo, se integra al ribosoma, ya que es una de las pocas estructuras con las que cuenta la célula procarionte.
Para la elaboración de esta estructura, puedes utilizar hojas de papel o periódico, café soluble y agua.
Con estas estructuras tienes los elementos mínimos para que tu modelo pueda representar a una célula procarionte. Como lo puedes ver. Teniendo tu modelo listo, ahora, se realizará una síntesis de lo estudiado en la sesión.
Entre las semejanzas se tiene, que tanto la célula eucarionte y procarionte poseen membrana celular, citoplasma y ribosomas. Y ambas células realizan todas las funciones vitales, como son la respiración, nutrición, relación con el entorno y reproducción, entre otras.
Por otro lado, para las diferencias podemos resaltar que la célula procarionte tiene ribosomas y plásmidos dispersos en el citoplasma. Y no cuenta con organelos rodeados por membranas. Además de que es mucho más pequeña que una célula eucarionte.
Así mismo, el material genético (ADN) se encuentra en forma circular y disperso en el citoplasma sin una membrana nuclear que lo delimite, mientras que en la eucarionte se encuentra dentro de la membrana nuclear.
De acuerdo con la teoría endosimbiótica propuesta por Margulis, las células eucariontes surgieron a partir de las procariontes. En esta propuesta se describe que posiblemente las mitocondrias y los cloroplastos fueron células procariontes independientes que en algún momento fueron absorbidas por otra célula más grande.
De esta manera surgieron los organelos celulares, que generaron la aparición de los primeros seres unicelulares eucariontes. En otras palabras, una célula vive dentro de otra célula y ambas se benefician de esta relación endosimbiótica.
Para concluir con esta síntesis revisa la siguiente lectura de Martín Bonfil Olivera del año 2004, titulada “¿Somos bacterias?”
“La idea puede parecer extraña. Después de todo, estamos acostumbrados a pensar en las bacterias, esos invisibles, microscópicos vecinos con quienes compartimos el planeta, como fuente sólo de enfermedades o de descomposición de los alimentos. O, en todo caso, como el último eslabón en el ciclo natural por el que la materia orgánica de los cadáveres regresa a formar parte del suelo.
Pero las bacterias son mucho más antiguas que nosotros. Estuvieron aquí en un principio, cuando no había ningún otro ser vivo sobre el entonces joven planeta. Sin duda los primeros organismos eran primitivas bacterias, con células de tipo procarionte: simples, sin un núcleo definido por una membrana, con su material genético en contacto directo con el citoplasma. En el origen fueron las bacterias. o sus ancestros.
Y es que, a su vez, las bacterias son nuestros ancestros. De nosotros los eucariontes, plantas, animales, hongos y ese quinto reino en que se agrupa a los organismos que no caben en los otros cuatro: los protistas.
La historia es simple. A lo largo de años, siglos, milenios y millones de años, las bacterias han venido creciendo, dividiéndose y multiplicándose. En este proceso también han cambiado. Evolución significa cambio. El azar de la mutación y el rigor de la supervivencia las han obligado a adaptarse a los ambientes más variados.
En algún momento de esta larga historia evolutiva, la competencia dejó de ser el único recurso, y la colaboración entró en escena. Quizá fue un accidente, quizá un intento fallido de conquista; lo cierto es que hoy las células eucariontes tienen en su interior lo que parecen ser antiguas bacterias…”.
Si quieres saber en qué concluye la lectura, se te invita a buscar este artículo en internet, ya que es de acceso libre. Así es, sólo coloca el nombre del autor en tu buscador de internet, “Martín Bonfil Olivera”, seguido del título “¿Somos bacterias?” y encontrarás la lectura. Se te invita leer y disfrutar de esta excelente lectura.
Como observaste, hoy se estudiaron dos conceptos importantes a lo largo de la sesión, pero se te invita a añadir uno de ellos a tu “Abecedario biológico”. El concepto de “célula procarionte” es el que se te pide que incluyas. No olvides: integrarlo, definirlo e ilustrarlo.
El reto de hoy:
En tu libreta escribe dos semejanzas y dos diferencias entre la célula procarionte y eucarionte. Si tienes la posibilidad, compártelo con tu profesora o profesor, así como con tu grupo de trabajo.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/


Login to join the discussion