La evolución en acción
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54Aprendizaje esperado: reconoce que el conocimiento de los seres vivos se actualiza con base en las explicaciones de Darwin acerca del cambio de los seres vivos en el tiempo.
Énfasis: recapitular los contenidos de este aprendizaje revisados en las sesiones anteriores.
¿Qué vamos a aprender?
Recapitularás los contenidos de las sesiones anteriores.
Seguramente cuando escuchas la palabra evolución, vienen a tu mente dinosaurios, fósiles e historias de personajes de otra época. Conocimientos aparentemente lejanos a ti.
En esta sesión reflexionarás acerca de ¿cómo a partir de las explicaciones asociadas a la evolución de las especies propuestas por Darwin y Wallace en el siglo XIX, la biología ha avanzado a pasos agigantados en el conocimiento de los seres vivos en el planeta y ha permitido el desarrollo de nuevas ramas científicas para su estudio?
¿Qué hacemos?
La sesión de hoy trabajarás con la información revisada anteriormente y con los términos incluidos en tu “Abecedario biológico”.
Empezarás con Lamarck. Recuerda a este personaje que dio pauta al fabuloso tema de la evolución.
A continuación, verás el bosquejo de un organizador gráfico, complétalo con los datos más relevantes. Es un sencillo mapa que vas a ir construyendo con las ideas más importantes.
Lamarck, formuló la primera teoría de la evolución.
En 1809 Publicó el libro “Filosofía zoológica” y “Sistema de animales invertebrados" en el que expuso su teoría evolucionista. Opinaba que las modificaciones en los seres vivos se dan como resultado del uso o desuso de determinado órgano. Formuló la Teoría de la evolución “La Herencia de los caracteres adquiridos”.
Lamarck, después del descrédito de su teoría. Pasó la última parte de su vida ignorado.
Fue hasta principios del siglo XX cuando se revisaron sus ideas, y se le comenzó a reconocer como un gran naturalista y pensador avanzado para su época. Hoy en día, se sabe que el uso o desuso de un órgano no es heredable.
La ciencia tiene esa característica, los argumentos científicos pueden y deben ponerse a prueba, si no resisten las pruebas son falsos, y si no pueden ponerse a prueba no son científicos.
Darwin y Wallace.
Wallace también tuvo un papel importante en la publicación de la teoría de la evolución por selección natural; pero él y Darwin, no fueron los únicos que contribuyeron a la construcción de esta Teoría.
Primero se describirá lo más relevante sobre Darwin, quien realizó un viaje que duró cinco años, como naturalista, alrededor del mundo, en el barco llamado Beagle. También realizó una expedición en el archipiélago de Galápagos, que fue todo un laboratorio para sus observaciones que sirvieron como base de su teoría.
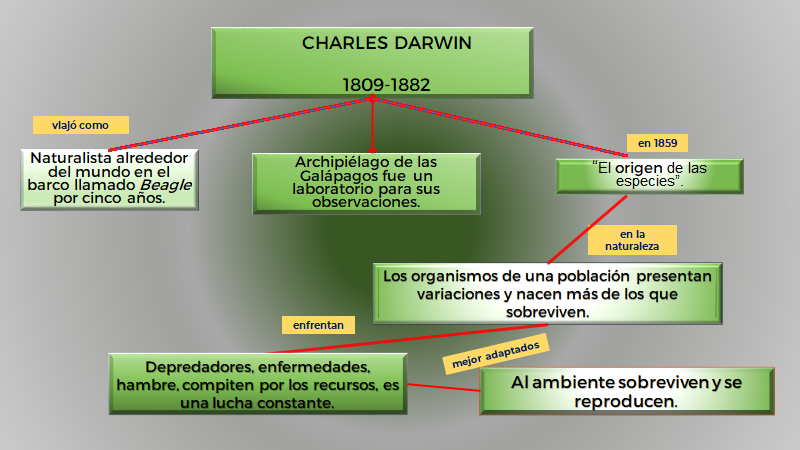
En 1859 publicó su libro titulado “El origen de las especies” donde expuso su teoría y ahí explicó que: en la naturaleza los organismos de una población presentan variaciones y nacen más de los que sobreviven, pues se tienen que enfrentar a depredadores, enfermedades, hambre, competir por los recursos, es una lucha en donde los mejor adaptados al ambiente sobreviven y se reproducen.
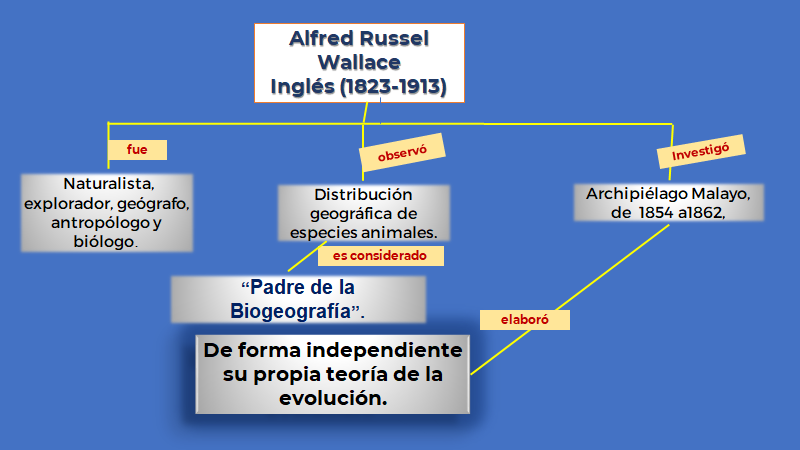
Alfred Russel Wallace, nació en 1823 y falleció a los 90 años en 1913. También era inglés, desde muy joven se dedicó a estudiar la naturaleza. Fue naturalista, geógrafo, antropólogo, biólogo y prácticamente la mayor parte de su vida, explorador. Observó la distribución geográfica de las especies animales por lo que es considerado el "padre de la biogeografía”. Realizó investigaciones en el archipiélago malayo, donde permaneció desde 1854 hasta 1862, esto le permitió elaborar de forma independiente su propia teoría de la evolución. En 1855, publicó un artículo en el que hablaba de la transformación de las especies.
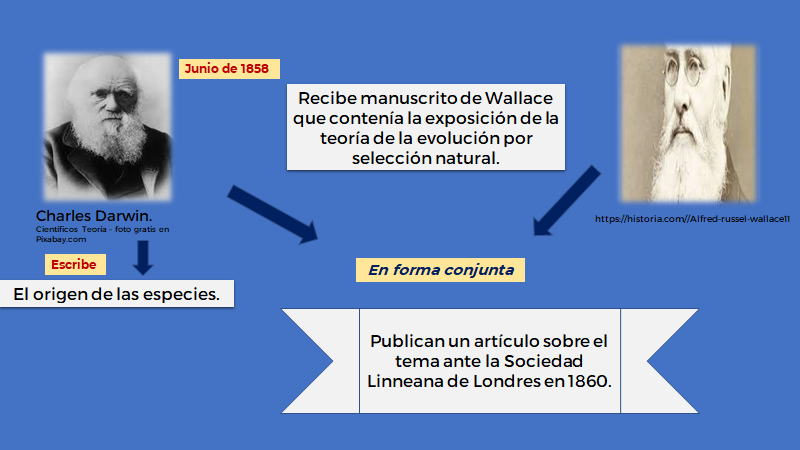
En junio de 1858, Darwin recibió un manuscrito de Wallace, que contenía la exposición de la teoría de la evolución por selección natural. Se le habían adelantado. A continuación, Darwin se puso a escribir un libro en el que plasmó sus ideas aportando una gran cantidad de datos. Había nacido: “El origen de las especies”.
La cuestión se solventó cuando ambos se pusieron de acuerdo y publicaron de manera conjunta ante la Sociedad Linneana de Londres en 1860, un artículo en donde propusieron una explicación evolutiva basada en la idea de selección natural.
Recordaste sus aportaciones, pero ¿cómo trascendieron en la historia?
Desde la muerte de Darwin en 1882, hasta principios del siglo XX el darwinismo se apagó lentamente. El no poder explicar los mecanismos de la herencia, parecía que condenaban a la teoría a su propia extinción.
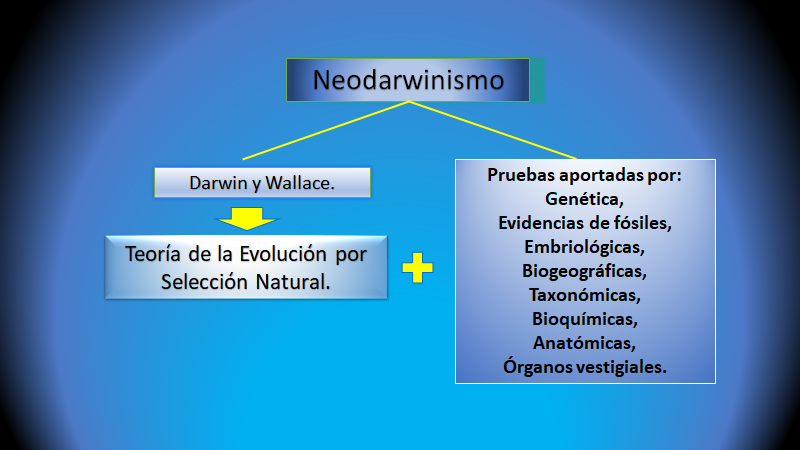
Sin embargo, el redescubrimiento de los trabajos de Mendel, sobre la herencia biológica, tema que se abordará en otro momento, hizo posible el resurgimiento del darwinismo. Fue hasta la década de los treinta del siglo XX que se integra la teoría de la evolución por selección natural como motor de la evolución, con las leyes de la herencia mendeliana. Ahora llamada Teoría sintética, también conocida como neodarwinismo, que ha sido enriquecida además con las leyes de la genética, y evidencias de distintas ramas de la Biología, como la Paleontología, Embriología, Biogeografía, Taxonomía, Bioquímica y Anatomía.

A más de 150 años después de su propuesta, la teoría de Darwin se ha convertido en el gran pilar de las ciencias de la vida.
De acuerdo con Theodosius Dobzhansky un genetista ruso del siglo XX, actualmente, en biología no hay nada que tenga sentido si no es a la luz de la evolución.
Recuerda ahora la información de los fósiles.
¿Por qué son importantes?
Por estas razones:
- Sirven para dar testimonio de la existencia de algunos seres vivos que habitaron el planeta hace millones de años, permiten conocer su morfología, distribución y modos de vida.
- Ayudan a comprender las variaciones climáticas y sus efectos en la flora y la fauna.
- Aportan información sobre especies ya extintas, y su relación con las actuales.
- Proporcionan información sobre periodos concretos de la historia de la Tierra y su formación.
Identifica los fósiles, ¡a ver qué tan hábil eres para encontrarlos! Recuerda a qué tipo de fosilización corresponden. Para complejizar el ejercicio la imagen será en blanco y negro.

¿Los encontraste?, ahora ve la imagen a color.

Seguro viste que se trata de: un fósil que tuvo un proceso de permineralización o también conocido como mineralización. Otro de impresión y un tercero de conservación en ámbar.
Variabilidad, es el siguiente concepto que revisarás.
La variabilidad es el conjunto de variaciones en el material genético de una población o especie.
Te acuerdas que Darwin decía que los individuos presentan variaciones o diferencias, pues está muy relacionado. En una población, por ejemplo, de la especie humana, fácilmente se pueden detectar variaciones, en estatura, color de cabello, estructura ósea, y demás, sin embargo, todos se parecen, pues pertenecen a la misma especie. De manera que los individuos de la misma especie nunca son idénticos entre sí, porque entre ellos hay variabilidad biológica, que es producto de la modificación genética, por lo que incluso dos hermanos son diferentes.
Lee el siguiente ejemplo:
En la boca, hay unas estructuras que la mayoría de los humanos padecen por ellas.
Actualmente en la especie humana las muelas del juicio son un enigma. Existen personas que nacen sin ellas, otra posibilidad es que no las desarrollan o también hay personas que, sí cuentan con ellas, aunque pueden no salir.
Los paleontólogos han estudiado por décadas, fósiles dentarios para interpretar los datos que puedan dar información de nuestros ancestros y la línea evolutiva. Actualmente la hipótesis más aceptada, dice que existía una gran variabilidad en la forma en que evolucionaron los dientes, incluyendo las muelas del juicio.
Sin embargo, existe otra hipótesis de la que recién se están obteniendo resultados, en donde se ven diferencias entre los Australopitecos y especies de nuestro género Homo. Los estudios confirman que los molares, incluidas las muelas del juicio, proporcionan información que hace que se pueda predecir el tamaño de dichos dientes por la denominada “cascada inhibitoria”. Que dice que el tamaño de un diente afecta a las dimensiones del que le sigue. Parece que hay un cambio específico en los dientes, cerca del origen de las especies del género Homo, que probablemente se relaciona con los cambios en la dieta blanda que tiene desde que cocina sus alimentos.
El volumen y tamaño de estos dientes ha disminuido considerablemente desde los Australopitecos hasta el Homo sapiens actual.
Como puedes observar en la siguiente imagen la mandíbula es cada vez menos prominente.
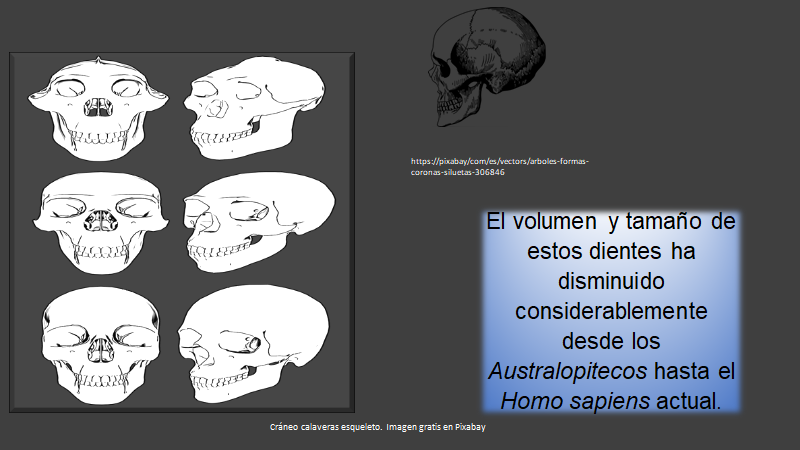
Parece que es la falta de espacio la fuente de los problemas que pueden ocasionar los terceros molares, entre los más frecuente están, infecciones, caries, abscesos o posición incorrecta, que daña al diente contiguo. Otro enigma es la aparición tardía de estas muelas, ya se sabe que cada diente, sea temporal o permanente tiene un tiempo predeterminado de erupción. Cuando son permanentes los dientes salen entre los 6 y 12 años. Hasta la adolescencia entre los 17 y 25 años aproximadamente suelen salir las muelas del juicio.
Si las muelas del juicio salen sin problema cumplen su función, triturar y moler para facilitar la digestión de los alimentos. Hay muchos casos en los que las muelas del juicio no pueden erupcionar y ahí aparecen los problemas. Investiga más acerca de este tema.
El siguiente concepto a revisar es Bacteria ¡Escherichia coli!, a través de ella se podrá explicar cómo interviene la adaptación, la selección natural y la evolución.
Lee con atención el siguiente caso y más adelante revisa las preguntas que se realizan.
Carmen llevó a su hija Mariana al médico con fuertes cólicos abdominales, náuseas, fiebre y diarrea, el doctor la cuestionó sobre la alimentación de su hija y Carmen comentó que evitan consumir alimentos en lugares públicos y que es muy cuidadosa al momento de elaborar los alimentos diarios.
Durante la consulta el médico preguntó sobre las actividades de Mariana.
Carmen contestó que la lleva a clases de regularización y a natación, y que en ninguno de esos lugares consume alimentos.
Una vez terminada la consulta el médico recomendó hacer un estudio de coprocultivo, en el que le detectaron la presencia de la bacteria Escherichia coli Con base en los resultados, el médico le recetó un antibiótico, un analgésico y electrolitos orales.
La bacteria que le detectaron a Mariana, es un microorganismo que vive en cada persona todos los días.
En 1885 fue descrita por primera vez por Theodore von Escherich, un bacteriólogo alemán y la denominó Bacterium coli commune, más tarde en 1954 se estableció el nombre de Escherichia coli, en su honor.
La E. coli, como también se le conoce, es una bacteria que habita en el intestino de la mayoría de los mamíferos sanos, entre ellos, los seres humanos, ¿notas por qué se dice que vive en cada persona?
Forma parte de los microorganismos que habitan en los intestinos y ayudan en la absorción de nutrientes y en la digestión. Existen varias cepas o colonias de bacterias, y gran parte de ellas son inofensivas, incluso la mayoría de las personas que contraen una infección por E. coli no desarrollan problemas graves y se recuperan por sí solas sin necesidad de tratamiento.
Entonces ¿por qué preocuparte por ella?
Resulta que algunas son patógenas, es decir, causan enfermedades en el ser humano como la cepa O157:H7, la cual produce una toxina, o sustancia tóxica, que daña el revestimiento interno del intestino grueso, lo que provoca fuertes dolores estomacales, vómito, cansancio, fiebre y diarrea.
Pero ¿cómo es que puede infectar al ser humano?
Por comer alimentos contaminados: carne poco cocida, frutas y verduras mal lavadas, bebidas no pasteurizadas, agua contaminada y se puede transmitir de persona a persona.
Afortunadamente existen medicamentos para combatir infecciones bacterianas ¡los antibióticos! que han permitido combatir infecciones que antes eran peligrosas y mortales, y hoy son fáciles de tratar.
Entonces ¿cuál es el problema? y, ¿qué tienen que ver la adaptación, la selección y la evolución en este caso?
El problema surge porque cada día las bacterias que causan infecciones, toman terreno frente a los antibióticos y éstos se vuelven menos eficaces o inútiles.
¿Por qué sucede esto?
Por el proceso de evolución al que están sometidas las bacterias.
Las bacterias se han adaptado a la intervención de los antibióticos, y predominan las que tienen resistencia.
El proceso de desarrollo de la resistencia a los antibióticos, es un proceso “evolutivo normal de los microorganismos”, pero se acelera por la intervención del ser humano. Al existir un uso inapropiado de ellos, es decir, cuando una persona que tiene infección por alguna bacteria interrumpe el tratamiento, al sentirse bien o no toma la dosis recetada.
Otra causa se debe al uso excesivo de antibióticos, por ejemplo, en la agricultura y ganadería que se suministra a los organismos de los que te alimentas. Lo anterior ha favorecido que se generen bacterias resistentes y que estas se diseminen.
Así que, por favor, no te recetes medicinas y si el médico te receta un antibiótico, sigue el tratamiento hasta terminarlo, para no contribuir a que las bacterias se hagan más fuertes.
La acción antibiótica es una presión ambiental que genera en las bacterias mutaciones al azar, y serán ventajosas para aquellas que a pesar de su acción logren sobrevivir y reproducirse, heredando este rasgo. El resultado será una generación de bacterias resistentes, a la presión del antibiótico.
¡Todo esto puede ocurrir en el interior de tu cuerpo!
Para comprender mejor el tema, observa la siguiente imagen:
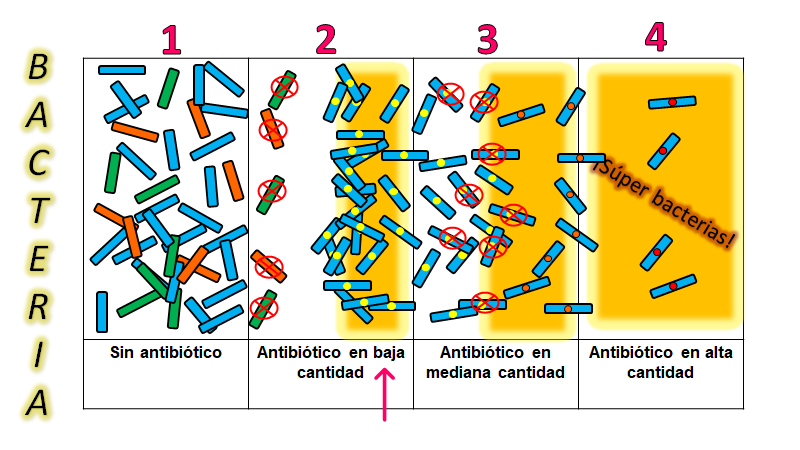
El recuadro que ves en la imagen está dividido en 4 espacios, cada uno con diferentes condiciones. Imagina que el recuadro es un recipiente conocido como caja de Petri con un caldo nutritivo que le permitirá a las bacterias alimentarse y reproducirse. Algunos espacios contienen antibiótico en distinta concentración, representado con el color amarillo, recuerda que éste evita que las bacterias sobrevivan.
El primer espacio, no tiene antibiótico y cuenta con una pequeña cantidad de bacterias de una colonia, representadas con colores: azul, verde y naranja, que indican la variabilidad que existe entre ellas. Al tener las condiciones adecuadas, estas se reproducen fácilmente.
Al terminarse el alimento, se desplazan al segundo espacio, pero ahora tienen un inconveniente: ¡el antibiótico! en baja cantidad, que impide su crecimiento. Algunas como observas no sobreviven, las de color verde y naranja. Sin embargo, mira lo que sucede, algunas bacterias presentaron mutaciones, que es un cambio brusco en su material genético, en este caso las de color azul con el punto amarillo, representa esa mutación, lo que les permite sobrevivir pese a la exposición al antibiótico.
Aquí viste cómo la teoría de Darwin se enriquece con los conocimientos de la genética, que él desconocía en su época, y ahora te permite ver que en la evolución no solo interviene la selección natural, sino también las mutaciones, entre otros factores.
La generación siguiente comenzó a desplazarse a la tercera zona, con mayor concentración del antibiótico y se repite el proceso, varias bacterias mueren, pero otras ya son más resistentes y otras, como ves, vuelven a mutar.
Una vez que se desplazan a la última zona puedes observar que hay gran concentración de antibiótico y a pesar de eso algunas bacterias logran sobrevivir y reproducirse, porque muestran cambios o mutaciones, con mayor tolerancia al antibiótico que se representa con el color del amarillo al rojo, es decir surgen ¡poderosas bacterias! con muy alta resistencia al antibiótico.
Entonces puede ser que determinado antibiótico ya no sea efectivo para esas “poderosas bacterias”, y los científicos deban investigar sobre nuevos antibióticos que puedan eliminarlas, esto implica tiempo, costos, y tecnología, que no hay en todas partes.
El ser humano ha acelerado la evolución de las bacterias, como viste, si no estuvieran expuestas a estas condiciones su evolución sería diferente.
Regresando al caso de Carmen y Mariana, y con base en la explicación revisa las siguientes preguntas.
- Si Carmen y Mariana se alimentan en casa ¿Dónde contrajeron la bacteria?
Nadando, ya que la bacteria está presente en agua contaminada por deshechos humanos, como es el caso de la mayoría de las albercas. - Si es normal y saludable que la bacteria Escherichia coli se encuentre en el organismo ¿Por qué Mariana se enfermó?
Porque algunas colonias de la bacteria Escherichia coli mutan y se vuelven patógenas generando infecciones en el ser humano. - ¿Por qué algunos antibióticos no son eficaces contra algunas bacterias?
Porque las bacterias, en este caso la E. coli, crean resistencia a los antibióticos como resultado de un proceso de evolución. - ¿Qué debe hace Mariana para evitar contagiarse nuevamente?
Verificar que las albercas que se visiten tengan las medidas sanitarias adecuadas. Lavarse las manos antes de comer y después de ir al baño. Evitar comer en lugares donde se dude de la limpieza en el tratamiento de alimentos. Consumir agua potable. Evitar el consumo de carne cruda o poco cocida.
Ahora revisa el concepto de ¡Selección artificial!, el cual debes agregar a tu “Abecedario biológico”.
La selección artificial, se denomina así, porque no se da de manera natural en el ambiente, sino que interviene el ser humano. Es un método de reproducción donde el ser humano, de acuerdo con sus necesidades, elige las características que desee de algunos organismos.
Un ejemplo de selección artificial muy común, es la domesticación de un perro.
Se cree que el perro fue el primer animal en ser domesticado, se ha investigado sobre su origen, y parece tener un antepasado común en el pequeño lobo del sudeste asiático. Para que la domesticación fuese posible, el hombre se encargó de seleccionar aquellos lobos que fueron sumisos ante él, y así sucesivamente con sus crías, hasta llegar a la gran variedad de perros de la actualidad. De hecho, el perro actual, conserva algunas características de sus parientes como, defender su territorio marcando algunos sitios o enterrando alimentos u objetos, ya que ellos entierran a sus presas muertas para asegurar su alimento. Todas las razas de perros a pesar de las variedades, que se observan, pertenecen a la misma especie: Canis familiaris.
¿Has escuchado que el mejor amigo del hombre es el perro?
Seguramente debe ser así, porque son utilizados con diferentes fines, como los siguientes: - Cuidan rebaños de diversos animales.
- Ayudan a cazar otros animales para alimento humano.
- Cuidan la seguridad de viviendas.
- Realizan tareas de rescate en protección civil.
- Apoyan a personas con debilidad visual e invidentes.
- Dan compañía, entre otros aspectos.
¿Tienes alguno en casa?
Observa algunos rasgos que el hombre ha utilizado a su favor con respecto al perro.
- Visión: son sensibles a objetos en movimiento y tienen excelente visión nocturna. Por ello en algunas culturas los usan para cazar.
- Oído: tienen un grado de movilidad de las orejas que les permite determinar rápidamente el origen de un sonido, los detectan a una distancia cuatro veces mayor que las personas.
- Gusto: pueden percibir sabores básicos y tienen la capacidad de asociar gustos con problemas de salud. Si algún alimento les hace daño lo evitarán en el futuro.
- Tienen colmillos para desgarrar carne cruda, por esta característica son utilizados para cazar.
- Olfato: su percepción de los olores es excelente, pues el cerebro canino es dominado por la corteza olfativa, de ahí que sean utilizados para buscar personas con tan sólo identificar su olor en alguna prenda.
- Músculos: Poseen músculos fuertes y resistentes.
El hombre y el perro, sin duda alguna, guardan una estrecha relación. Pero el hombre no solamente ha intervenido en la reproducción de los perros, también lo ha hecho con otros organismos, por ejemplo, las frutas, verduras, cereales, y animales como el cerdo, el caballo, y las diversas especies de ganadería.
El día de hoy has reflexionado cómo se ha ido construyendo la teoría de la evolución por selección natural, con la participación de muchos científicos desde épocas pasadas y actuales. Así como el trabajo y el estudio constante que permitió sus logros
El reto de hoy:
Observa a distintos gatos e identifica los rasgos que el humano ha seleccionado, a través de su crianza, para tenerlo como mascota. Para ello, elabora un dibujo o un esquema, donde indiques las características de los gatos que los hace especiales y queridos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas



Login to join the discussion