¡México, país de las maravillas!
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54Aprendizaje esperado: explica la importancia ética, estética, ecológica y cultural de la biodiversidad en México.
Énfasis: reconocer la importancia estética y cultural de la biodiversidad en México.
¿Qué vamos a aprender?
Explicarás la importancia ética, estética, ecológica y cultural de la biodiversidad en México y lo harás mediante reconocer la importancia estética y cultural de la biodiversidad en México.
¿Qué hacemos?
Algo que caracteriza a la nación es su gastronomía; con riquísimos platillos gracias a los grandes aportes de la biodiversidad mexicana.
Sabías que el maíz con el que hacen las tostadas, ¿no es la única variedad que existe? Te imaginas ¿cuántas variedades de maíz existirán?

https://search.creativecommons.org/photos/9e37db5b-a0a5-44cd-81bb-87a10598ed86
Observa el siguiente video para abundar en el tema. Mientras ves el video, anota en tu cuaderno las ideas que consideras importantes y que te ayudarán a entender más sobre este tema.
- Maíz: de México para el mundo.
https://www.youtube.com/watch?v=1n6QQXU6b1g&t=188s&loop=0&start=00:00&end=02:55
Como viste en el video existen muchas variedades de maíz y 64 de ellas son cultivadas precisamente, en las milpas de México. Además, la milpa te brinda otros alimentos para preparar tostadas y quesadillas, entre otros tipos de comida.
Tal vez te preguntes, ¿acaso la milpa aporta, más que maíz?
La respuesta es afirmativa, la milpa mexicana, además de maíz, es uno de los medios que aporta alimentos, y que están presentes en más de un platillo de los que consumes diariamente.
¿Cuáles son esos alimentos que además del maíz, aporta la milpa mexicana?
Revisa la siguiente imagen.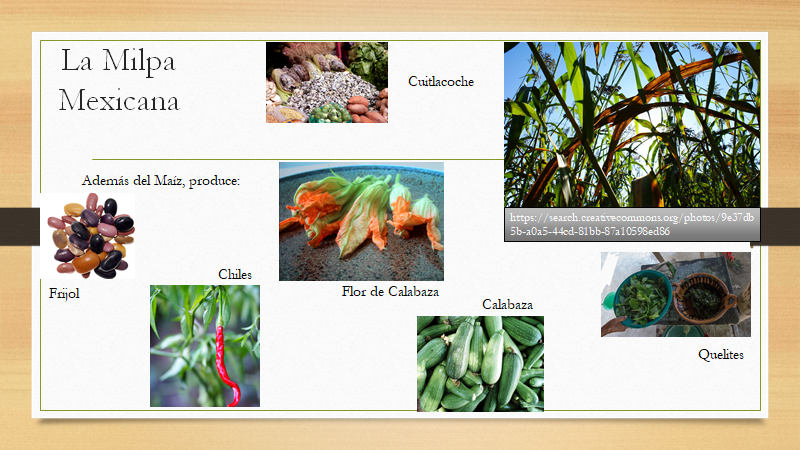
Uno de los alimentos es el frijol, que, además de ser base de la dieta mexicana, en los sembradíos de maíz, ayuda a fijar una sustancia llamada nitrógeno, mediante la participación de unas bacterias conocidas como nitrificantes que fertilizan la tierra y nutren al maíz, si no se cultiva el maíz junto con el frijol, habría desgaste del suelo de la milpa, lo que podría provocar que ya no se pudiera cultivar. Una cuestión similar ocurre con el chile, ingrediente de platillos típicos, la flor de calabaza, la calabaza y los quelites.
Además, en la milpa también se produce ¡el cuitlacoche!
El huitlacoche o cuitlacoche, del náhuatl “cuitlatl – excrecencia y cochtli – dormido” es un tipo de hongo que crece en el maíz.
El ser humano lo aprovecha en la cocina por su delicioso sabor y valor nutricional. Tanto, que en el mundo gastronómico se ha llegado a considerar como “la trufa mexicana”. ¿Cómo ves?
México cuenta con muchas maravillas, por lo que se identifica, como un país megadiverso, con una riqueza natural e invaluable. Tanto, que influye no solo en la comida, sino también en sus tradiciones y costumbres.
Entonces, ¿la biodiversidad no solo influye en lo que comes?, ¿hay más ámbitos a los que aporta?
Existen más ámbitos, donde la riqueza natural, aporta, algo más que solo lo gastronómico. Un ejemplo, es como la percibes, tus hábitos, tus costumbres y tus tradiciones que favorecen la organización y convivencia de las sociedades.
Lee el siguiente cuento, ahí podrás ver cómo una cultura percibe o integra la biodiversidad.
“EL MAIZ Y LA ARRIERA”
De: Mario Aburto Castellanos
“Casi todos conocemos a la hormiga arriera: cabezona, con patas largas y fuertes y una cintura muy delgada.
Hace mucho, cuando la gente todavía no conocía el maíz, la arriera era la única que lo sembraba y, en lugar de ser flaquita, tenía la forma regordeta de uno de sus granos.
En ese tiempo existió Leonel, un hombre que era más fuerte que los demás y aprovechaba
su fuerza para obligar a los otros a obedecerlo.
—¡Me darán todos los alimentos que junten
y yo los repartiré como quiera! —ordenaba,
mientras la gente trabajaba como hormiga
y le obedecía por temor.
Leonel vigilaba a las personas cuando recogían las frutas de los árboles, atrapaban peces y cazaban animales, para que no fueran a guardarse nada.
Un día que el fortachón estaba atento a otra cosa, la gente, ya harta, planeó:” Es muy fuerte, pero si unimos nuestras fuerzas acabaremos con su dominio, ¡vamos por él!”.
En el campo, Leonel veía cómo una arriera cargaba granos de maíz hasta su agujero.
—¿De dónde has sacado esos granos? —le preguntó.
—Es un secreto —contestó la hormiga y siguió con su trabajo.
—¡Te ordeno que me lo digas! —le gritó Leonel.
—Tendrías que hacer algo muy bueno para que te contara el secreto —contestó la arriera.
Leonel enfureció, envolvió a la hormiga con uno de sus largos cabellos y empezó a
apretarle la cintura mientras gruñía: —¡Dímelo o no te soltaré!
La arriera gritaba de dolor, y estaba casi a punto de confesar cuando se escucharon
unas voces: —¡Oye, tú, suéltala!, ¡no dejaremos que abuses de nadie más!
Al ver tanta gente inconforme y decidida, Leonel sintió miedo, soltó a la hormiga y salió huyendo para nunca más volver.
En agradecimiento, la hormiga les reveló el secreto del cultivo y la cosecha del maíz, para que tuvieran otra forma de alimentarse.
Desde entonces se cultivan las milpas y se comen tortillas, tamales, gorditas y elotes, y
la hormiga arriera tiene una cintura tan delgada que parece que se va a partir en dos”.
Fin.
Es fascinante cómo la biodiversidad puede influir en la identidad de un pueblo o una nación. ¿No lo crees?
Observa el siguiente video sobre cómo influye la biodiversidad en la construcción de la identidad cultural mexicana. - Biodiversidad e Identidad
https://www.youtube.com/watch?v=9mU7fS1UUiw
¿Qué te pareció el video?
Es grandioso saber que la biodiversidad ha permitido concebir la identidad de tu nación desde distintos ámbitos. La humanidad ha utilizado a la naturaleza para su desarrollo e identidad. Por ejemplo, el Escudo Nacional, incorpora elementos naturales que representan valores y te recuerdan el origen e historia de tu país.
La cultura mexicana integra esa riqueza en distintas tradiciones, entendiendo que, por estas formas de convivencia, se construyen las comunidades.
Realiza la siguiente actividad en tu cuaderno. Identifica tres costumbres o tradiciones que se realicen en tu comunidad o región. Para ello, elabora un cuadro que contenga los siguientes aspectos
-Costumbre o festividad.
-Flora o fauna que se utiliza o festeja.
-Significado de la festividad.
-¿En dónde se lleva a cabo?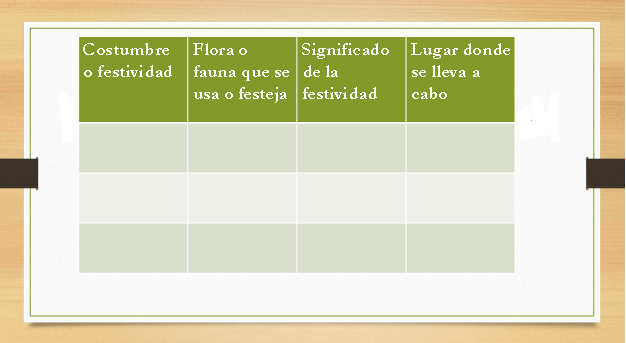
Toma en cuenta que, si no conoces o recuerdas alguna de ellas, puedes pedir ayuda a un familiar o amigo. Por lo general, las personas que llevan bastante tiempo viviendo en un mismo lugar, conocen mejor las festividades y tradiciones de la comunidad.
La biodiversidad permite que exista diversidad cultural y propia, enriqueciendo a la nación con múltiples grupos étnicos. Para conocer la cantidad de grupos étnicos en tu país y su aporte a tu identidad nacional, revisa el siguiente video. - La diversidad cultural de México
https://www.youtube.com/watch?v=COLJ-oXwB70
¿Notaste cuánta diversidad cultural existe en tu país?
Hay tanto de qué hablar con relación a lo que aportan los grupos étnicos, pero primero debes conocer que la cultura es un conjunto de formas, expresiones, costumbres, vestimenta, religiones, comidas, rituales y maneras de ser, que caracterizan y dan identidad. Por ello, la importancia cultural se refiere a cómo el medioambiente influye, moldea y transforma a una sociedad y sus prácticas. La biodiversidad motiva a crear tradiciones y costumbres.
¿Tú conoces qué tradiciones, costumbres y festividades se llevan a cabo en tu región o comunidad?
Cada comunidad, municipio o estado, tiene particularidades en cuanto a sus festejos y tradiciones.
Observa la siguiente imagen.

¿De qué festividad se trata?
Se trata del día de muertos, donde las calaveritas de chocolate y las flores de cempaxúchitl son características.
Mira esta otra imagen.

Es una imagen de las Fiestas Patrias.
México cuenta con muchas cosas que de seguro en el mundo lo han de observar con gran interés. La estética propia de nuestro pueblo, que se expresa a nivel internacional debe ser símbolo de orgullo para cada mexicana y mexicano.
Vale la pena mencionar ¿qué es la estética?, ya que tal vez, te puedas estar haciendo esta pegunta, así como saber ¿cuál es la relación qué tiene la estética con la biodiversidad y su correlación en la construcción de una cultura?
La estética se refiere a la manera particular que tiene cada persona de percibir, entender y apreciar a la naturaleza. Es decir, el gusto y la emoción que te provoca el contacto con el entorno natural y social. Lo estético se refiere a la percepción de la belleza de la biodiversidad mexicana, y cómo la cultura se apropia de ella.
Tu deber como ciudadana o ciudadano es preservar tu biodiversidad, y promover las tradiciones y costumbres que te caracterizan como mexicano en este caso.
Ahora retomarás los conceptos que vas a agregar a tu “abecedario biológico”. Uno tiene relación con las tradiciones y costumbres de una comunidad como la vestimenta o la comida. ¿Sabes cuál es?
La cultura.
El siguiente concepto tiene que ver con la forma de percibir la belleza natural. ¿Ya identificaste qué concepto es?
La estética.
Estos son los dos conceptos que agregarás a tu abecedario biológico. Recuerda buscar la definición de cada uno, o bien a partir de lo que hoy aprendiste, para que realices tu propia definición.
El reto de hoy:
Imagina que tienes un amigo en el extranjero y le envías una pequeña carta. Escríbela en tu libreta de Ciencias. Biología. En esa carta resalta una tradición o costumbre típica de tu comunidad o región. Apóyate en el cuadro de costumbres y tradiciones que hiciste durante esta sesión.
Recuerda retomar el concepto cultura, y describe en tu carta, la región a la que pertenece la tradición o costumbre de la que estás escribiendo; resalta qué elementos de la biodiversidad se emplean. Asimismo, considera el concepto estético para detallar cómo es apreciada la festividad por las distintas comunidades de tu región. Qué sentidos y emociones se propician al celebrarla.
No olvides elaborar tu carta, con los materiales que tengas a la mano y recuerda la importancia que tiene el uso de dibujos para hacerla más llamativa y por supuesto, utiliza tu creatividad.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas


Login to join the discussion