Por una mejor salud, sumemos nutrientes y restemos calorías.
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54Aprendizaje esperado : explica cómo evitar el sobrepeso y la obesidad con base en las características de la dieta correcta y las necesidades energéticas en la adolescencia.
Énfasis: reconocer las necesidades energéticas en la adolescencia.
¿Qué vamos a aprender?
En la sesión de hoy trabajarás con el aprendizaje esperado:
Explica cómo evitar el sobrepeso y la obesidad con base en las características de la dieta correcta y las necesidades energéticas en la adolescencia.
Y el propósito es:
Reconocer las necesidades energéticas en la adolescencia.
En esta sesión titulada: Por una mejor salud, sumemos nutrientes y restemos calorías.
Para ello, debes recurrir a tus materiales escolares y tener a la mano tu “Abecedario biológico”, imprescindible en cada sesión.
¿Qué hacemos?
Observa lo que dice el maestro Raúl de Tonalá, Jalisco, quien estará participando en esta sesión mediante una serie de videos.
-
Maestro Raúl 3
Se debe mencionar que esto no implica por sí mismo la disminución o eliminación de los problemas de sobrepeso y obesidad, sino que solamente contribuye a la creación de un ambiente saludable que fomente un mejor estilo de vida.
-
Maestro Raúl 4
Observa la duda que planteó un alumno con respecto a la alimentación.
“He visto que algunos de mis familiares eligen productos bajos en azúcar o en grasas, ya que comentan que son más saludables y que a la vez nos ayudarán a evitar el sobrepeso y la obesidad ¿Esto es cierto?”
Recuerda que al hablar de dieta correcta se refiere al consumo de alimentos con cantidades adecuadas de proteínas, carbohidratos, lípidos, vitaminas, minerales y agua simple potable.
Además, es cierto que en el mercado existen muchos productos que se promocionan como “dietéticos”, “bajos en azúcares” y bajos en grasas o lípidos, lo cual realmente no significa que sean bajos en energía.
Por lo que podrías comentarles a tus familiares están en lo correcto al elegir productos bajos en azúcares o en grasas, pues efectivamente son más saludables. Sin embargo, también conviene recordar que no hay nada mejor que el consumir alimentos basados en el Plato del Bien Comer, realizar actividad física con regularidad, de tal manera que las kilocalorías que ingieras estén acordes con dicha actividad, tu edad y sexo, esto les permitirá mantener un estilo de vida saludable y un peso correcto.
-
Maestro Raúl 6
Y para reconocer si un producto procesado como una bebida azucarada o cualquier otro alimento influirá en el desarrollo de enfermedades alimentarias, debes recordar que el cuerpo en todo momento requiere de la energía de los alimentos para su funcionamiento, aunque no se esté haciendo ejercicio alguno, ya que el respirar, digerir o dormir también representa un gasto de energía.
Cualquier alimento que se consuma, tendrá energía, excepto el agua simple potable. La energía contenida en los nutrientes de los alimentos se mide en calorías (cal), aunque es más frecuente la kilocaloría (kcal). Un gramo de carbohidratos y de proteínas contienen 4 kilocalorías de energía, en cambio un gramo de lípidos contiene 9 kilocalorías.
-
Maestro Raúl 7
Para reconocer cuánta energía es la que necesita, se han creado tablas que estiman la cantidad aproximada de kilocalorías que requerirían consumir de acuerdo a su edad, sexo, estatura y peso.
Observa la tabla que se muestra a continuación e identifiquen la cantidad de energía que necesitan según su edad y actividad física.
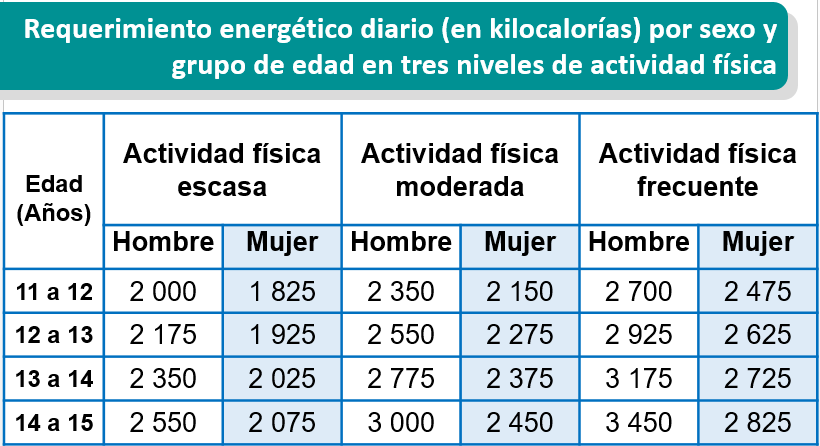
Por ejemplo, puedes ver que en la primera columna se muestran los rangos de edad en los cuales te puede ubicar. Después, se muestran tres columnas que clasifican la actividad física diaria en tres tipos: Escasa, Moderada y Frecuente.
-
Maestro Raúl 8
¿Ya identificaste cuál es tu tipo de actividad física?
Observa de nuevo la tabla.
Debajo de cada uno de los tipos de actividad física se encuentra el sexo de la persona y al cuadrar la edad, con la actividad física y el sexo, podrás identificar la cantidad de kilocalorías que necesitarías para mantener el correcto funcionamiento del organismo.
Debes tomar en cuenta que estos valores pueden variar de persona a persona, ya que la genética, la estructura corporal y distintas enfermedades pueden hacer que estos valores sean diferentes para cada persona.
-
Maestro Raúl 9
Por lo tanto, es mejor buscar otras opciones como las aguas de sabores naturales como limón o jamaica, que además de ser bajas en azúcares y calorías, ayudarán a tu cuerpo a metabolizar mejor los azúcares de una fruta de temporada que el de un edulcorante artificial.
Observa otra pregunta que realizó otro alumno.
“He visto que en la televisión promocionan muchos productos para bajar de peso, como pomadas, fajas o pastillas. ¿Me podría decir si estas son opciones recomendables para bajar de peso para nosotros los adolescentes?”
-
Maestro Raúl 11
Ahora, para llevar un seguimiento aproximado de la cantidad de kilocalorías que consumirías por los alimentos que conforman tu dieta, observa la siguiente tabla, en la cual muestra el aporte kilocalórico aproximado por cada porción de alimentos.
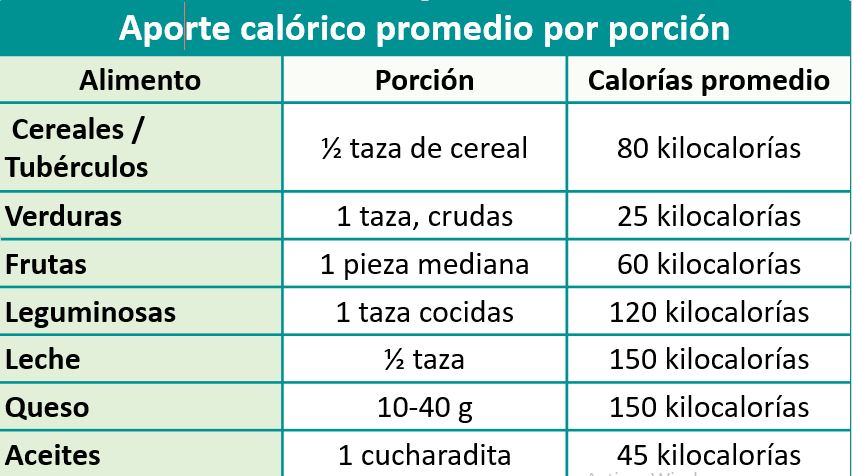
Como puedes observar, en el caso de los cereales y leguminosas, como el arroz, el maíz, la avena o el trigo, en forma de sopa, tortillas, cereal de caja, granola, barras energéticas, nos aportan 80 kilocalorías por media taza. En el caso de que desees comer un poco más, la energía se multiplicaría.
Piensa entonces ¿Cuántas porciones de cada alimento estás consumiendo? ¿Serán las sugeridas para esta etapa de tu desarrollo?
-
Maestro Raúl 12
Ahora, para identificar cuánta energía gastas en las actividades que realizas al día o en la semana, observa las siguientes imágenes que muestran la cantidad de kilocalorías que una persona de 50 o 60 kilogramos gastaría en 30 minutos continuos de ejecución.
Para dormir necesitarías 26 kilocalorías, al ver la televisión sólo se utilizarían 27 y para estudiar sólo se requerirían 30. Para lavar trastes necesitaríamos 56 kilocalorías por 30 minutos.
Si durante el día realizas actividades físicas más intensas, puedes reconocer que caminar lento necesita 77 kilocalorías, trapear 98, bailar 152 así como el caminar rápido nos consume 146 kilocalorías.
En caso de que la actividad física sea intensa o vigorosa, se sabe que el jugar futbol o basquetbol te resultará un gasto energético de 210 kilocalorías, el andar en bicicleta a una alta velocidad requiere de 250, el correr 227 y el subir escaleras 381.
¿Cuáles de ellas son las que realizas frecuentemente? y ¿Cuántas kilocalorías estarías gastando para realizar estas actividades?
-
Maestro Raúl 13
Es de suma importancia que las y los adolescentes consuman suficiente vitamina A, vitamina D, vitaminas del complejo B, calcio, hierro y zinc, por lo que se recomienda la ingesta diaria de algunos vegetales verdes y alimentos de origen animal como la carne, huevo y lácteos.
-
Maestro Raúl 14
En esta sesión identificaste los requerimientos calóricos que necesita el cuerpo según tu sexo, edad y el tipo de actividad física que desarrolles.
Recuerda que una dieta correcta debe ir acompañada de actividad física; por ello es necesario que acumules 30 minutos al día. Puedes iniciar con periodos de cinco a diez minutos e incrementar poco a poco el tiempo.
Ahora, es momento de agregar una nueva palabra al “Abecedario biológico”
La palabra es “kilocaloría”, recuerda anotar su definición, así como ilustrarla.
El reto de hoy:
-
Maestro Raúl 16
Si un día decidieras consumir los tres productos súper procesados que más te agradan, ¿Cuántas kilocalorías te aportarían? ¿Qué actividades físicas deberías hacer y por cuánto tiempo para poder quemar estas kilocalorías? ¿De qué manera esta información te ayudaría a mejorar tus hábitos de consumo?
¡Buen trabajo!
Gracias por tu esfuerzo. 
Para saber más:
Lecturas
https://libros.conaliteg.gob.mx/secundaria.html




Login to join the discussion