Paquetes de la herencia
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:54
Aprendizaje esperado: escribe la importancia, funciones y ubicación de los cromosomas, genes y ADN.
Énfasis : reconocer la ubicación e importancia de los cromosomas.
¿Qué vamos a aprender?
En esta sesión continuarás con el aprendizaje esperado: “Describe la importancia, funciones y ubicación de los cromosomas, genes y ADN.”
Cabe destacar que, en esta ocasión, el propósito será:
“Reconocer la ubicación e importancia de los cromosomas”, a través de las actividades que vamos a desarrollar en la sesión titulada: “Paquetes de la herencia”.
Recuerda que los materiales escolares son importantes en cada sesión, como lo es tu cuaderno, libro de texto, bolígrafos y un lápiz.
Además, no olvides tener a la mano tu “Abecedario biológico” para que anotes, definan e ilustres la palabra que seleccionarás.
¿Qué hacemos?
En la sesión anterior revistaste que la célula es la unidad básica, estructural y funcional de todo ser vivo. Y que, en las células eucariontes se encuentra un organelo muy importante llamado núcleo, en el cual está almacenada toda la información genética de un organismo.
Dicha información está contenida en el ADN que se encuentra disperso en el núcleo, formando una especie de red llamada cromatina. Al empezar la división celular, el ADN se enrolla y forma unas estructuras llamadas cromosomas, los cuales sólo son visibles durante el proceso de división celular sea por mitosis o meiosis.
Para poder estudiar estas estructuras, los científicos esperan hasta que la célula empieza su proceso de división, ya que de esta manera pueden ver con mayor claridad su composición y cantidad.
Durante la mitosis o meiosis, los cromosomas mantienen al ADN enrollado apretadamente alrededor de unas proteínas con apariencia de carretes de hilo llamadas histonas, lo que le permite a la célula transmitir su información genética de forma más ordenada hacia su descendencia durante la división celular.
Cabe resaltar que los cromosomas preservan el contenido genético y evitan, en lo posible, que se dañe o se extravíe. Es decir, garantizan la transmisión de la información genética almacenada en el ADN de la célula madre a sus descendientes.
El término cromosoma deriva de las palabras griegas chroma (color) y soma (cuerpo). Los científicos dieron este nombre porque son estructuras celulares que se tiñen de color oscuro con algunos de los tintes utilizados en el laboratorio y generalmente tienen forma de equis.
¿Sabías que los cromosomas varían en número y forma entre los seres vivos?
Por ejemplo, la mayoría de las bacterias tienen uno o dos cromosomas circulares.
En cambio, los organismos con células eucariontes, como los seres humanos, junto con otros animales, plantas, hongos y protistas, tienen cromosomas lineales en forma de equis que se ordenan en pares dentro del núcleo de la célula.
Los cromosomas presentan una estructura doble, compuesta por dos formas largas, paralelas entre sí, llamadas cromátidas, también conocidas como cromátidas hermanas, ya que una de las cromátidas tiene un fragmento del ADN original y la cromátida hermana contiene una copia exacta de esta información. Esto ayudará a que, al separarse las cromátidas, se herede la misma información del ADN a cada una de las células hijas durante la división celular.
Cada cromátida está compuesta por un número determinado de genes, los cuales se localizan en un lugar específico, facilitando su ubicación y estudio.
Las cromátidas están unidas entre sí en un punto focal llamado centrómero.
El centrómero de los cromosomas divide cada cromátida en dos segmentos, llamados “brazos”: uno corto (Maestra pega el título) y uno largo. Y dependiendo de la ubicación del centrómero estaremos en presencia de diferentes formas de cromosomas. Como las que puedes ver a continuación en la imagen.
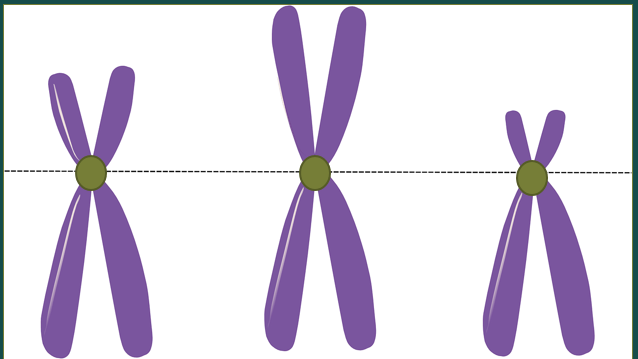
Cabe recordar que la cantidad y forma de los cromosomas son diferentes entre las distintas especies.
Observa la siguiente imagen.
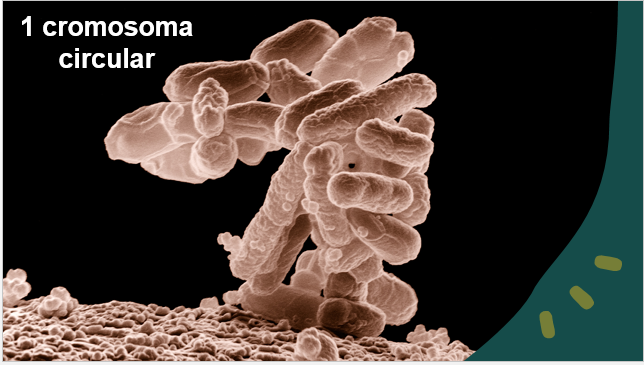
Este tipo de cromosomas es característico de las células procariontes.
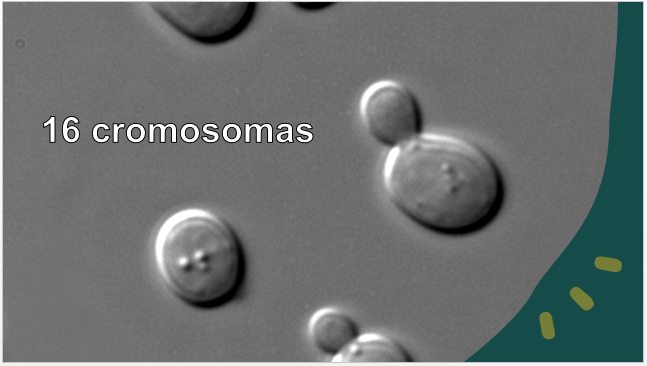
El de la levadura, que es un hongo. Menciona que sus células eucariontes contienen 16 cromosomas.
Los perros tienen 78 cromosomas, en tanto que la especie humana tiene 46 cromosomas.
De acuerdo con las investigaciones hechas sobre los cromosomas, un número mayor de cromosomas no implica mayor complejidad. Por ejemplo, en el reino Plantae se pueden encontrar especies vegetales con pocos cromosomas como los chícharos, con 7 cromosomas; y especies con muchos cromosomas como los helechos quienes llegan a tener hasta 1260.
De hecho, cuando los científicos se dieron cuenta que los cromosomas almacenan ADN, empezaron a analizarlos, ver sus semejanzas y diferencias, ordenándolos en parejas, por tamaño y considerando la ubicación del centrómero. A esta representación gráfica se le denominó Cariotipo.
Los cromosomas se ordenan por parejas, con el brazo corto hacia arriba. Posteriormente se ordenan por tamaños -de mayor a menor-, y dentro de un tamaño semejante, por la posición del centrómero.
En los organismos de reproducción sexual, como en el caso de la mosca de la fruta o la especie humana, existen cromosomas sexuales diferenciados y tienen dos formas: “X” o “Y”. Estos pueden colocarse en el grupo que les corresponde por tamaños o bien ubicarse formando el par sexual separados de los autosomas (cromosomas no sexuales).
Los autosomas son el conjunto de cromosomas no sexuales del organismo, que intervienen en la transmisión de todas las características físicas y genéticas, excepto las que están vinculadas con el sexo.
Mientras que los cromosomas sexuales son el par de cromosomas que determinan el sexo.
En este sentido los seres humanos tienen 22 pares de autosomas y un par de cromosomas sexuales, en el número 23.
En el cariotipo, los cromosomas se ordenan por parejas, esto da pie otra pregunta. ¿Por qué el cuerpo humano tiene pares de cromosomas semejantes?
Esta semejanza se presenta porque contienen la información de los mismos genes, en idéntico orden.
Y una persona tiene dos, porque uno nos fue heredado por el padre y otro por la madre, durante la fecundación.
A estos cromosomas se les denominan cromosomas homólogos ya que tienen la misma información genética, pero al heredar un gen de cada progenitor estos pueden tener distintas expresiones de la misma característica, por ejemplo, que tu padre te herede el color de ojos marrón y tu madre el color de ojos azul.
Los genes que determinan esto inciden en la misma característica: el color de ojos, pero con una variante: ojos marrón o azul.
Cuando se empiezan a formar los óvulos o espermatozoides, en el proceso de división celular llamado meiosis, los cromosomas homólogos que están en el núcleo de la célula, se emparejan y recombinan durante la meiosis a través del entrecruzamiento.
En este proceso los cromosomas intercambian fragmentos de información, lo que producirá diferencias genéticas entre las células de los gametos. Esto es fundamental para promover la variación genética entre la descendencia.
¿De qué manera los cromosomas sexuales determinan el sexo del nuevo organismo?
Para analizarlo, observa estos dos cariotipos humanos.
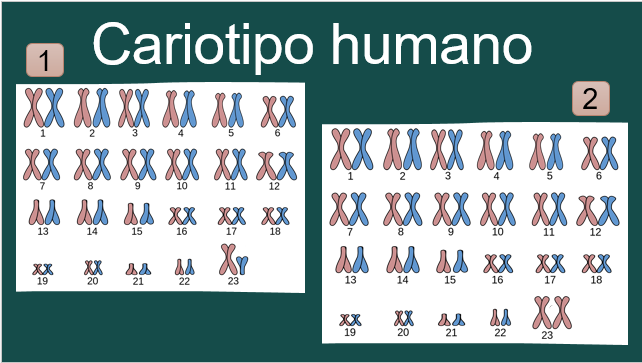
Ya están ordenados como se describió anteriormente, y puedes ubicar a los autosomas y a los cromosomas sexuales.
Se muestran dos cariotipos porque uno corresponde al sexo femenino y otro al masculino.
¿Sabes cómo puedes distinguirlos? Busca las semejanzas y diferencias.
Cómo pudiste reconocer, los primeros 22 pares son iguales, estos son los autosomas. Pero en el par 23, es donde se encuentra la diferencia que distingue al sexo femenino del sexo masculino. A este último par se le conoce como cromosomas sexuales.
El sexo femenino tiene dos cromosomas “X”, mientras que el masculino tiene un cromosoma “X” y uno “Y”. Los cromosomas sexuales, son muy diferentes, no sólo en apariencia sino también en tamaño y composición genética.
¿Cómo se heredan estos cromosomas?
Todas las células de los seres humanos sean nerviosas, musculares, de la piel o de los huesos, contienen los 46 cromosomas; la única excepción son los gametos (óvulos y espermatozoides), que contienen la mitad, 23 cromosomas.
Un espermatozoide con 23 cromosomas, fecunda a un óvulo, con 23 cromosomas para producir un nuevo organismo con el total de la información genética que necesita, que en este caso son 46 cromosomas.
Como el descendiente recibe la información hereditaria de ambos padres, no es genéticamente idéntico a ninguno de ellos, pero presenta varias semejanzas con cada uno.
Debes recordar que, durante la formación de los espermatozoides u óvulos, se dividirá en dos la cantidad de cromosomas.
Al finalizar la meiosis, en los óvulos siempre encontraras una X como cromosoma sexual, pero en los espermatozoides, algunos llevarán cromosoma X y otros Y. Dependiendo de cuál espermatozoide sea el que fecunde al óvulo, se determinará el sexo de la descendencia.
Entonces son los cromosomas sexuales masculinos, que al azar determinan el sexo del bebé.
Con lo anterior se puede concluir que gracias a la información genética almacenada en los cromosomas dentro de nuestras células, se definen todas nuestras características.
A pesar de ser tan pequeños, tus 23 pares de cromosomas contienen toda la información que definirá cada una de tus características físicas.
Si llegara a ocurrir algún cambio en el número o en la forma de los cromosomas, esto puede afectar el desarrollo del organismo y generar diversos padecimientos.
Un caso concreto, es el Síndrome de Down. Este síndrome, también llamado trisomía 21, se presenta cuando se hereda una copia de más en el par del cromosoma 21.
Al tener esta alteración cromosómica, las personas presentan características físicas distintivas que incluyen débil tono muscular, boca pequeña que se mantiene parcialmente abierta, porque no tiene espacio suficiente para la lengua, y párpados de forma peculiar.
Otro ejemplo, es el Síndrome de Turner.
En esta alteración, la persona tiene sólo un cromosoma “X” en el par sexual. Como se puede observar en el modelo de cariotipo.
Sus efectos son más notorios en la pubertad, ya que la deficiencia de hormonas impide que las niñas desarrollen las características sexuales secundarias y casi todas las mujeres con el síndrome de Turner carecen de óvulos maduros, lo cual impide que tengan hijos. Normalmente tiene mayor riesgo de sufrir enfermedades cardiovasculares y pérdida del oído.
Con esto se puede observar la importancia de los cromosomas para el desarrollo de los organismos.
En esta sesión identificaste qué son los cromosomas, su ubicación y estructura.
Así mismo, comprendiste que todos los seres vivos tienen una cantidad específica de cromosomas. Entre los que se incluyen los autosomas y los cromosomas sexuales.
En el sexo femenino en el par 23 se encuentran dos cromosomas sexuales X, mientras que en el masculino uno es “X” y el otro “Y”.
Los cromosomas que contienen los mismos genes se llaman homólogos. Y si llega a existir alguna alteración en el número de cromosomas, se pueden presentar Síndromes como el de Down o el de Turner.
Retoma el concepto de “Cromosoma” para agregarlo a tu “Abecedario biológico”. Busca la definición en tu libro de texto, en un diccionario o en internet. Después elabora la imagen representativa para que lo puedas recordar más adelante y lo retomes en la elaboración de su modelo.
El reto de hoy:
Investiga en tu libro de texto, en internet o alguna otra fuente de información, la estructura del cromosoma, puedes retomar la que conociste el día de hoy.
Elabora un modelo considerando las principales partes de su estructura. Para ello es recomendable usar material que tengas en casa o reciclar. Aplica y desarrolla tu creatividad.
Al finalizar comparte tu investigación y modelo con familiares y si es posible con tu maestra o maestro y compañeras y compañeros.
¡Buen trabajo!
Gracias por tu esfuerzo. 
Para saber más:
Lecturas
https://libros.conaliteg.gob.mx/secundaria.html


Login to join the discussion