Figuras y cuerpos geométricos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:51
Figuras y cuerpos geométricos
Aprendizaje esperado: construye configuraciones con formas, figuras y cuerpos geométricos.
Énfasis: identifica características específicas en figuras y cuerpos geométricos.
¿Qué vamos a aprender?
Construirás configuraciones con formas, figuras y cuerpos geométricos.
Identificarás características específicas en figuras y cuerpos geométricos.
Pide a tu mamá, papá o algún adulto que te acompañe en casa que te apoyen a desarrollar las actividades y a escribir las ideas que te surjan durante esta sesión.
¿Qué hacemos?
¿En alguna ocasión has observado un cubo? ¿Cómo es? Al observar el cubo identifica que está formado por varios cuadrados, cuenta cuántos son. El cubo está formado por 6 cuadrados.
Estos cuadrados son los que se llaman caras del cubo, ahora que ya sabes que el cubo está formado por cuadrados, arma un cubo.
Coloca un cuadrado abajo, para que sea la base; va un cuadrado. Luego otro cuadrado para uno de los lados, van dos cuadrados, coloca otra cara del cubo.
Ya llevas tres cuadrados. Otro cubo del otro lado, ya son cuatro cuadrados. Continúa colocando más cuadros hasta poner uno arriba para cerrar el cubo. Listo, ya está tu cubo armado y utilizaste 6 cuadrados para el cubo.
Cada cubo tiene 6 caras y cada una de éstas se forma con un cuadrado. Recuerda que el cubo es un cuerpo geométrico.
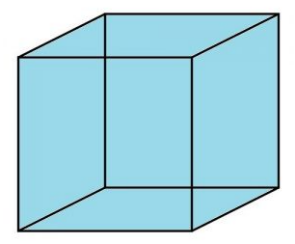
Fuente: https://www.caracteristicass.de/cubo/
¿Qué otros cuerpos geométricos puedes construir con las figuras que conocemos? En una sesión anterior, construiste algunos cuerpos geométricos, como un cubo, cono, cilindro, prisma rectangular, pirámide cuadrangular y esfera.
Para construir un prisma rectangular. ¿Qué figuras necesitas? Este cuerpo geométrico está formado por 6 rectángulos. Cuatro rectángulos son largos y dos son más pequeños, que se ubican en los extremos del prisma. ¿Qué objetos has observado que tengan la forma de este prisma?
Observa el siguiente video para conocer sobre los prismas rectangulares.
- Prismas rectangulares.
https://youtu.be/n_74tHekV9s?t=550
Del minuto 9:10 a 9:37
Realiza un prisma. ¿Con qué lo puedes armar? Puedes utilizar algunos palillos y plastilina, si no lo tienes no te preocupes, con ayuda de un adulto, busca un material que puedas utilizar para formar tu prisma.
Para armar un prisma rectangular, forma un rectángulo largo como base, después realiza tres rectángulos largos para los otros lados. Finalmente arma dos rectángulos más pequeños para cada extremo del prisma.
Descubre que para este cuerpo geométrico utilizas rectángulos de diferentes tamaños, ahora hay que armar la pirámide con base cuadrada. Observa con atención este cuerpo geométrico.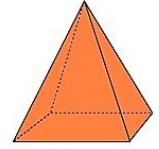
Fuente: https://www.geogebra.org/m/xrpnd22c
¿Ya sabes qué figuras geométricas necesitas?
¿Cuántas caras tiene esta pirámide?
Observa dos pirámides que realizaron tu compañero Juan.
Fuente: https://es.slideshare.net/yakelintenorio/exposicin-pirmides
Compáralas con el modelo. ¿Se parecen?
Formo la base de la pirámide con un cuadrado, después, armó cuatro triángulos para las demás caras de la pirámide. Los triángulos que formó tienen un lado corto y dos más largos, por eso mi pirámide quedó muy alta. ¿Cómo te quedó tu pirámide? Y si algún día quisieras armar un cono, ¿Qué figuras debes utilizar?
Fuente: https://www.universoformulas.com/matematicas/geometria/cono/
Observarlo con mucha atención, la base del cono es un círculo y una de sus características es que termina en punta. Observa que el cilindro, a diferencia del cono, tiene dos bases circulares.
Fuente: https://ar.pinterest.com/pin/359584351503419673/
Los círculos deben ser del mismo tamaño. ¿Qué objetos conoces que tengan forma de cilindro? Observa el siguiente video para que conozcas más sobre esta figura geométrica. - Cilindros.
https://youtu.be/n_74tHekV9s?t=1264
Del minuto 21:04 a 21:18
Es momento de un juego para identificar las características de los cuerpos geométricos.
Para jugarlo pídele al adulto que te acompaña que te lea la descripción del cuerpo geométrico y observa con mucha atención los objetos que te rodean. La primera en encontrar un objeto con la forma del cuerpo geométrico descrito alza la mano, muestra el objeto y explica por qué lo eligió.
Ejemplo la primera descripción: Este cuerpo geométrico está formado por 6 caras, cada cara es un cuadrado. Esta descripción, ¿A qué cuerpo geométrico corresponde? Es un cubo y el dado tiene forma de cubo, una caja de regalo también es un cubo, tiene 6 caras y cada una es un cuadrado.
Siguiente descripción, este cuerpo geométrico está tiene una base circular. En la parte superior tiene una punta, esta descripción, ¿A qué cuerpo geométrico corresponde? Es un cono, y el gorro de cumpleaños tiene esa forma: la base circular y arriba tiene una punta. ¿Encontraste otro objeto en forma de cono?
La siguiente descripción es: Este cuerpo geométrico no tiene lados, toda su forma es en curva. Esta descripción, ¿A qué cuerpo geométrico corresponde?
Es una esfera y un objeto puede ser una esfera navideña, no tiene lados y toda su forma es en curva. ¿Qué otro objeto puede tener la forma de esfera? La pelota tampoco tiene lados y toda su forma es en curva.
Otra descripción sería: Este cuerpo geométrico tiene como base un cuadrado. Cuatro de sus caras son triángulos, esta descripción, ¿A qué cuerpo geométrico corresponde?
Es una pirámide. Arturo encontró un rompecabezas con esa forma, el cuadrado y los triángulos.
Sigue jugando.
Este cuerpo geométrico está formado por 6 caras, tiene cuatro rectángulos grandes y en sus bases dos rectángulos chicos. Esta descripción, ¿A qué cuerpo geométrico corresponde? ¡Es el prisma rectangular!
Un bloque de madera puede tener esa forma, tiene 6 caras, cuatro rectángulos son grandes y dos pequeños. ¿Hay otro objeto con esa forma? Un cartón de leche tiene forma de prisma rectangular.
La última descripción. Este cuerpo geométrico tiene bases circulares y esos círculos son del mismo tamaño, esta descripción, ¿A qué cuerpo geométrico corresponde? A un cilindro.
Un vaso tiene dos círculos del mismo tamaño en sus bases, o una lata, también tiene dos círculos de igual tamaño.
Con este juego porque pudiste identificar algunas características de los cuerpos geométricos.
Este día aprendiste que, utilizando figuras, puedes armar cuerpos geométricos. Los cuerpos geométricos, al igual que las figuras, están en los objetos que te rodean.
El reto de hoy:
Te invitamos a seguir descubriendo más cuerpos y figuras geométricas. ¿Has observado la taza en la que tu mamá toma su café?
¿Te has dado cuenta a qué cuerpo geométrico se parece tu colchón?
Observa tu vaso de agua, ¿A qué cuerpo geométrico se asemeja?
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/K1MAA.htm

https://libros.conaliteg.gob.mx/20/K2MAA.htm



Login to join the discussion