¡Alerta, zona de riesgo!
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:49Aprendizaje esperado: identifica zonas y situaciones de riesgo a las que puede estar expuesto en la escuela, la calle y el hogar
Énfasis: conoce zonas y situaciones de riesgo en la calle y en la escuela.
¿Qué vamos a aprender?
Identificarás zonas y situaciones de riesgo a las que puede estar expuesto en la escuela, la calle y el hogar.
Pide a tu mamá, papá o algún adulto que te acompañe en casa que te apoyen a desarrollar las actividades y a escribir las ideas que te surjan durante esta sesión.
¿Qué hacemos?
¿En alguna ocasión tomando agua has querido hablar? ¿Qué sucedió? Posiblemente no has logrado hablar, en otras ocasiones te ha dado tos, debes tener mucho cuidado cuando estés bebiendo o comiendo algo y evitar hablar o jugar al mismo tiempo, porque te puedes ahogar.
¿Has vivido una experiencia así? ¿Qué has hecho en estos casos? ¿Qué sentiste? ¿A quién pides ayuda? Pregúntales a tus papás, ¿Cómo han auxiliado a sus niñas y niños ante una situación así?
Precisamente hoy conocerás algunas zonas y situaciones de riesgo, lo que se acaba de comentar es una de ellas.
Para empezar, vas a reconocer algunas situaciones que pueden ser de riesgo. ¿Cómo lo vas a hacer?
Observa varias imágenes de lugares y situaciones de riesgo, e identifica qué situaciones pueden llegar a ser riesgosas, a estas imágenes les debes colocar un tache para las situaciones de riesgo y una paloma las que no lo son.
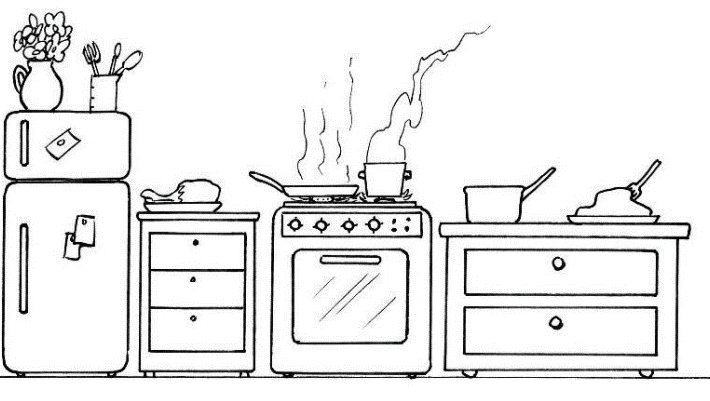
Fuente: https://www.educima.com/dibujo-para-colorear-cocina-i8200.html
¿Este es un lugar de alto riesgo en el hogar? ¿Por qué piensas que es riesgoso? La cocina es riesgosa, porque hay cuchillos, fuego y otras herramientas que pueden ser peligrosas.
Se encuentran en este lugar utensilios entre otras cosas y con la ayuda del adulto que te acompaña vas a ir identificando cuál es el riesgo que implican.
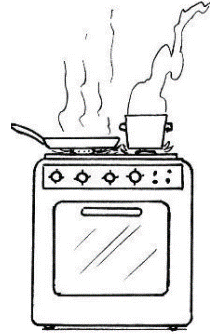
Fuente: https://www.educima.com/dibujo-para-colorear-cocina-i8200.html
https://www.imagui.com/a/dibujos-de-estufas-de-cocinas-para-colorear-i6epXez85
¿En cuál de estas dos imágenes, observas que hay un riesgo? Tu compañero Carlos considera que la estufa con la flama encendida, porque si se acerca a la estufa cuando está encendida, puede quemarse.
También puede suceder que si hay una olla con comida que está caliente se puede caer y quemarte. Si tu mamá está cocinando y brinca el agua o el aceite también te puedes quemar.
Coloca un tache a la estufa encendida y una palomita en la estufa apagada. ¿Qué otra situación de riesgo crees que suceda en la cocina?

Fuente: https://www.cehipar.es/tipos-de-cuchillos-de-cocina/
Los cuchillos son utensilios que se deben utilizar con mucha precaución. Las niñas y los niños siempre tienen que utilizarlo cuando un adulto se los proporcione y siempre bajo su supervisión. ¿Utilizas cuchillos bajo la supervisión de un adulto? ¿Has tenido alguna situación de riesgo con cuchillos? ¿Qué fue lo que sucedió?
Debes tener mucho cuidado cuando ayudas a tu mamá o papá a preparar algunos alimentos.
Coloca un tache en la imagen. Observa las últimas imágenes.
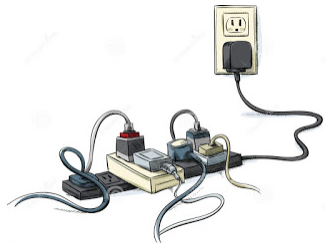

Fuente: http://factoresderiesgosst.blogspot.com/p/riesgos-macanicos.html
Tu compañero Alan dice que esto sí que es de mucho riesgo, pero no debería de serlo, si se usa de manera correcta.
¿Has tenido algún accidente con los contactos de luz? ¿Crees que es un buen lugar para jugar? ¿Por qué?
Nunca debes jugar ni tratar de introducir ningún objeto dentro de los contactos, ya que es muy peligroso, siempre debes pedir la ayuda de un adulto para conectar algún aparato. Coloca un tache en esta imagen.
También en las escuelas, puede haber zonas de riesgo, aunque la escuela es un lugar seguro, debes evitar situaciones de riesgo y hacer acuerdos para no tener accidentes.
¿Qué situaciones de riesgo existen en la escuela? Observa las siguientes imágenes.


Fuente: https://pt-br.facebook.com/portoneshipolitogarcia130/posts/puertas-y-ventanas-para-escuelas/1623791411217364/
¿Por qué crees que las puertas de la escuela son riesgosas? ¿Cómo las utilizas? ¿Será acaso que las azotas? ¿Qué puede suceder si juegas con las puertas?
Mariana cree que puede suceder un grave accidente, como machucarse y lastimarse los dedos o la mano. Coloca un tache o paloma, según corresponda.


Fuente: https://isie.sonora.gob.mx/component/content/featured.html?id=featured
Recuerdas una medida de seguridad en este espacio. No debemos tirar agua y jabón para evitar resbalones, pero en esta ocasión hay otros riesgos.
Se ha sabido de niñas y niños que ¡se suben a los lavabos y esa es una forma incorrecta de utilizarlos porque se ponen en riesgo. ¿Cómo utilizas los lavabos? ¿Qué sucedería si te subes a ellos?
Es importante saber que los lavabos se utilizan únicamente para lavar, lavarse las manos, lavar los pinceles o algún otro material, no es un lugar para jugar.
Una recomendación muy importante es que, si están ocupando los lavabos, hacer una fila para esperar tu turno, así como cuando tu mamá se forma en la fila de las tortillas.
Las últimas imágenes.


Fuente: https://www.pinterest.com.mx/carmen1189/imagenes-de-actividades-en-kinder/
https://www.freepik.es/vector-gratis/nino-jugando-columpio_1020128.htm
¿Has jugado en los columpios? ¿Cómo lo utilizas? En los parques y en algunas escuelas hay columpios, son muy divertidos, pero se puede volver riesgoso si no sabes utilizarlo de manera correcta.
Tienes que estar acompañado de un adulto, escuchar con atención las indicaciones para su uso y si es necesario formarte para esperar tu turno.
Si ves un juego como este y está lleno de niñas y niños, ¿Qué haces? ¿Te subes? ¿Te subes a otro juego? ¿Esperas tu turno?
Es muy interesante y útil esta sesión. Con estas recomendaciones te servirá para evitar riesgos en la casa y en la escuela.
En esta sesión pudiste identificar que los lugares no son riesgosos por sí solos, a veces con las acciones los volvemos peligrosos, así que hay que utilizarlos de manera correcta y así evitamos accidentes.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas



Login to join the discussion